上章回顾和本章内容

上一章名称为Plaxis远程脚本教程二——实体对象及其参数(板)，介绍了如何查看文档创建和计算Plaxis中的板实体单元，并给出了相关脚本参考文档。

本章将继续分析Plaxis中的实体单元土工格栅和embedded桩，并通过Python脚本实现自动化的创建与分析。

2土工格栅(Geogrid)

土工格栅是一种铺嵌入在土体中的一种土体加固结构。在Paxis2D中为一种线实体，在Plaxis3D中为一种面实体。

在Plaxis2D中创建土工格栅效果如下图所示，在实际的Plaxis建模中一般被渲染成黄色：

在Plaxis3D中创建土工格珊效果如下图所示，其中红色部分即为土工格栅：

2.1实体特性及其用途

官方文档中对土工格栅实体单元的描述如下：

Geogrids are slender structures with an axial stiffness but with no bending stiffness. Geogrids can only sustain tensile forces and no compression. These objects are generally used to model soil reinforcements.

根据官方文档的表述，土工格栅在PLaxis中是一种不考虑厚度，但是在另外两个方向上有轴向刚度但没有弯曲刚度的一种结构。该结构只能承受拉力而不能承受压力，一般用于模拟加筋土的力学特性。

在Plaxis2D中土工格栅在划分网格时一般做成5节点或3节点线单元，具体是5节点或3节点取决于土体的单元节点书。当土体单元为15节点时对应为5节点线单元；当土体单元为6节点时对应为3节点单元。

在Plaxis3D中土工格栅在划分网格时一般做成6节点三角形单元，每个节点包含在x,y,z方向上的3个位移自由度。

土工格栅在土体中的作用与与钢筋在混凝土中的作用类似（胡文韬老师），一般起限制土体的对挡土结构的挤压变形的作用。由于土工格栅属于抗拉构件，一定程度上可以使得土体产生一定的抗拉强度，可以通过限制张拉力的大小以模拟土工格栅结构的失效。

2.2参数与算法

土工格栅的主要参数受材料的弹塑性模型影响，包括两个方向上的抗拉刚度 E${{\rm{A}}_x}$ ，两个方向上的最大张拉力${N{p,1}}$和${N{p,2}}$，在Plaxis3D中增加了抗剪刚度参数GA，同时在不考虑热效应的情况下可以勾选各向同性，勾选各向同性后两个方向上的抗拉刚度E${A_1}$和E${A_2}$相等。在不考虑热效应的情况下具体参数描述如下表所示：

属性名	描述	计算公式或取值方法
Elasticity	定义材料的弹性或弹塑性	0:弹性，1：弹塑性，2：弹塑性(N~$\varepsilon $，3：粘弹性)
IsIsotropic	定义材料的各向同性	True：各向同性，False：非各向同性
E${A_1}$	一个延伸方向上的抗拉刚度，在Plaxis中为X方向上的抗拉刚度	单位：kN/m
E${A_2}$	另一个延伸方向上的抗拉刚度	若勾选了各向同性则等于E${A_1}$
${N_{p,1}}$(弹塑性模型)	一个延伸方向上的最大张拉力，在Plaxis中为x方向上的最大张拉力	单位：kN/m
${N_{p,2}}$(弹塑性模型)	另一个延伸方向上的最大张拉力	若勾选了各向同性则等于${N_{p,1}}$
GA(3D)	剪切刚度，若土体发生了垂直土工格栅面的剪切变形可以一起抗剪	单位：kN/m

在Plaxis2D和3D中的材料参数介绍文档如下所示：

• Plaxis2D —PlateMat2D
• Plaxis3D —PlateMat3D

其中，各向同性属性IsIsotropic属性与Plate板实体单元的各向同性属性类似也是难以勾选上。经测试，在Plaxis2D中需要同时输入EA1和EA2两个属性，且保证这两个属性相等才能正确勾选上。在Plaxis3D中，需要同时输入EA1、EA2和GA三个属性，且满足EA1==EA2==2GA时各向同性属性才会被勾选上。

相比于Plate实体单元来说，土工格栅实体单元的参数简单很多，且经过测试所有的属性都可以正常赋值。土工格栅属于抗拉构件，起本构关系可以设置为弹性模型、弹塑性模型和粘弹性模型等，应当根据实际需要合理选择。

土工格栅在建模中和在计算中均不计算其厚度，即其于土体共同变形但不存在与土体搭接的情况。

Python接口及调用方法

在Plaxis2D中土工格栅通过线单元进行创建，在3D中土工格栅通过面单元进行创建。基于以上和第一章的内容，不再演示GUI界面中创建土工格栅的命令，直接介绍如何使用python脚本进行土工格栅的创建。

使用Python在Plaxis2D中创建土工格栅

土工格栅在Plaxis2D中为线实体单元，因此首先需要创建线对象，后基于创建的线对象创建土工格栅。Python代码流程如下所示：

# 在(30, -1)和(40, -1)的位置创建一条线段，由于Plaxis会先创建两个点然后再绘制线段，因此线段为line命令的最后一个元素
GeogridLine = g_i.line((30, -1), (40, -1))[-1]

# 基于创建的线创建土工格栅
geogrid = g_i.geogrid(GeogridLine)

创建土工格栅的材料集，并将上一步创建的土工格栅赋值材料属性：

# 创建土工格栅的材料，这里使用弹性各向同性材料属性，此时的各向同性可以被正常勾选
geogridMat = g_i.geogridmat('MaterialName', '土工格栅', 'Elasticity', 0,
                            'IsIsotropic', True, 'EA1', 10E7, 'EA2', 10E7)

# 将上一步创建的土工格栅材料赋值到创建好的土工格栅中
geogrid.Material = geogridMat

至此，在Plaxis2D中的土工格栅模块创建完毕。如果需要修改材料参数的话，比如将EA1修改为10E8：

# 修改创建的土工格栅材料参数
geogridMat.setproperties('EA1', 10E8)

修改参数之后的效果如下图所示：

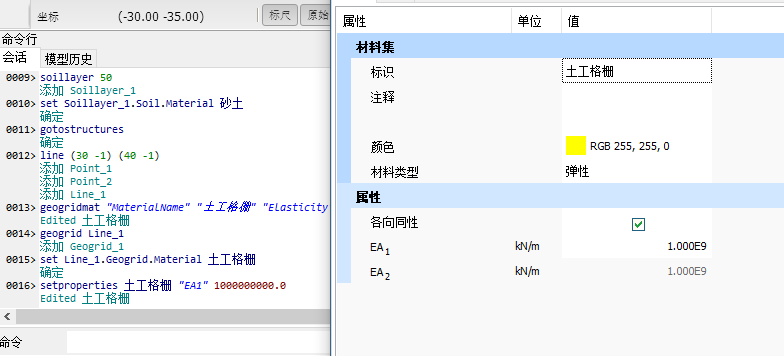
基于在创建材料集时已经勾选了各向同性选项，因此在此处修改EA1后，同时EA2也会同步发生变化。

使用Python在Plaxis3D中创建土工格栅

土工格栅在Plaxis3D中为面实体单元，因此需要创建面对象，后基于创建的面对象创建土工格栅。Python代码流程如下图所示：

# 创建一个多边形体，以下示例创建了一个以(0, 0, 0), (-8, 0, 0), (-8, -8, 0), (0, -8, 0)四个点为角点的正四边形
GeogridSurface = g_i.surface((0, 0, 0), (-8, 0, 0), (-8, -8, 0), (0, -8, 0))

我们对这个多边形体进行详细的分析，首先对生成的多边形执行输出操作，如下所示：

# 输出多边形对象
print(GeogridSurface)

>>> <Polygon {255788FB-CB53-47FB-9198-14A9C2404A6B}>

可以看到输出结果为一个多边形对象，但是多边形对象其本身是一个可以迭代的点集列表，该数组又四个点组成，四个点对应了多边形的四个角点，如下图所示：

# 输出多边形对象的长度
len(GeogridSurface)

>>> 4

# 迭代输出多边形对象中的内容
for i in GeogridSurface:
    print(i)

>>> <HelperPoint {EE73AFD0-EBAA-486B-965F-E33AC241316C}>
>>> <HelperPoint {A1433843-FCBA-48C1-A6BD-40CDA83A07E1}>
>>> <HelperPoint {C956DBEC-F074-4B7E-BE97-CD8BD4E7B9F6}>
>>> <HelperPoint {93D25443-94A8-4A58-9B73-ECB44C783802}>

根据输出可以看到，多边形对象本质是由四个点组成，这四个点分别对应多边形的四个角点，且各个角点之间使用直线进行连接。下面对各个角点的坐标进行输出：

# 迭代输出多边形中角点坐标
for i in GeogridSurface:
    print(i.x, i.y, i.z)

>>> 0 0 0
>>> -8 0 0
>>> -8 -8 0
>>> 0 -8 0

做好多边形后，从创建的多边形中创建土工格栅：

# 从创建好的多边形中创建土工格栅
geogrid = g_i.geogrid(GeogridSurface)

创建土工格栅的材料，并应用到创建的土工格栅上：

# 创建一般各向同性弹性材料，EA设为10E8，GA为EA的一半
geogridMat = g_i.geogridmat('MaterialName', '土工格栅', 'Elasticity', 0,
                            'IsIsotropic', True, 'EA1', 10E7, 'EA2', 10E7, 'GA', 50E6)
# 将材料应用到土工格栅上
geogrid.Material = geogridMat

计算结果输出类型

完成结构计算之后，我们需要查阅输出的计算结果，和Plate对象类似，土工格栅对象也不能直接在上面选取曲线点，而是有专门的输出对象ResultTypes.Geogrid。Plaxis2D和Plaxis3D中的土工格栅输出对象的文档分别如下所示：

• Plaxis2D——ResultTypes.Geogrid
• Plaxis3D——ResultTypes.Geogrid

通过文档可以得到土工格栅有很多类型的属性可以获取，通过调用getresults方法来得到计算结果。如需要获取土工格栅的每个节点的全部位移，可以参考如下代码：

# 获取土工格栅上所有节点的总位移
g_o.getresults(geogrid, phase1, g_o.ResultTypes.Geogrid.Utot, 'node')

该方法接收4个传入参数：geogrid需要提取计算结果的土工格栅对象，phase1需要提取计算结果的计算阶段，g_o.ResultTypes.Geogrid.Utot需要获取的总位移结果类型，node指定获取实体单元上的节点计算结果，可选应力节点stress point。

3Embedded桩(Embedded Beam)

Embedded桩在Plaxis2D和3D中均为线单元实体，一般用于锚杆与土层的连接过渡。在Plaxis中的模型示意图如下图所示：

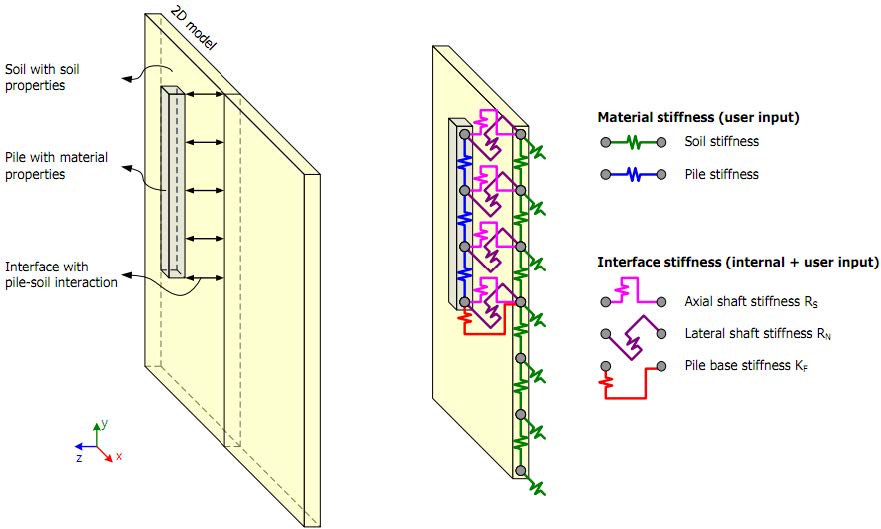
但是为什么在上面又翻译成Embedded Beam呢，因为该实体单元的受力形式与土木工程结构意义上的Beam是相同的，因此将Embedded桩翻译成Embedded Beam（从文档里面抄的~）

3.1实体对象及其用途

Embedded桩是一种考虑桩土相互作用的线性实体单元，可以用作模拟基坑锚索的嵌固层、灌浆体和桩基础。该实体单元可以考虑桩土之间的摩擦作用，同时也考虑桩头在持力层的嵌固作用。同时该实体单元可以承受弯矩，能够模拟桩在土中受到的非均匀外荷载。

该实体单元在Plaxis文档中的描述如下所示：

An embedded beam is a structural object (such as a pile, rock bolt or grout body) composed of beam elements that can be placed in arbitrary direction in the sub-soil and that interacts with the sub-soil by means of special interface elements. The interaction may involve a skin resistance as well as a foot resistance.

根据官方的文档的描述，Embedded桩是一个有厚度可以承受弯矩的圆柱形线性实体单元。在计算时embedded桩的简化形式同土工格栅一样，与土单元的划分形式有关。当土体单元为6节点单元时，embedded桩简化为3节点性单元；挡土提单元为15节点单元时，embedded桩简化为5节点单元。

embedded桩适用于模拟对土体造成有限扰度的桩类型，包括钻孔桩、挤密螺纹桩等。但并不是适用于所有类型的桩，如果有些桩对土体的土压力系数或桩侧摩阻力影响显著的话，需要进一步评估具体的模拟方法。

3.2embedded桩的建模特性

embedded桩可以用于模拟桩基础和锚杆或锚索的嵌固部分，因此对于不同的模型形式，embedded两端节点的连接方式对其力学特性也存在较大的影响。

由于emmbedded桩他是一个有厚度的线单元，因此在考虑它本身自重的计算时，Plaixs会将其考虑与土体搭接，搭接部分为embedded桩的所有体积。搭建后的重力修正计算公式同板的计算公式。

3.2.1embedded桩的力学特性选择

在Plaxis2D或3D中创建了embedded对象之后，可以在选择浏览器(select explorer)中选择所创建的embedded桩的力学特性表现。有以下几种类型可以选择：桩、锚杆、注浆体。如下图所示：

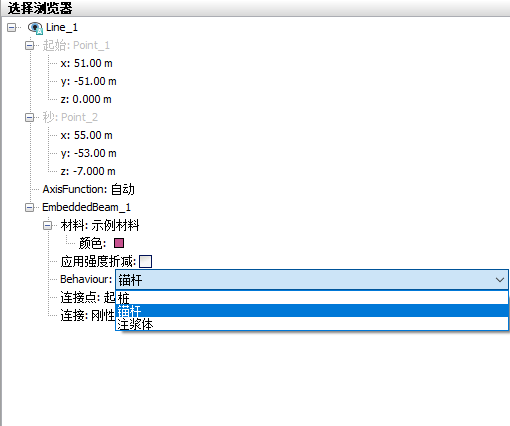
当选择为力学行为为桩时，其连接点的下拉菜单有两种选择：顶部和底部，如下图所示：

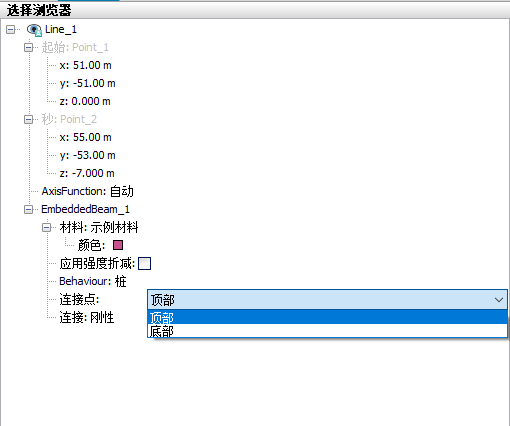
其中顶部指的是桩在竖直的情况下，桩身中Z坐标值最大的位置，若桩身水平，则顶部则为桩身x坐标或y坐标最小值的位置。底部的定义与顶部的定义相反。

当选择力学行为为锚杆时，其连接点的下拉菜单中有两种选择：First和Second，如下图所示：

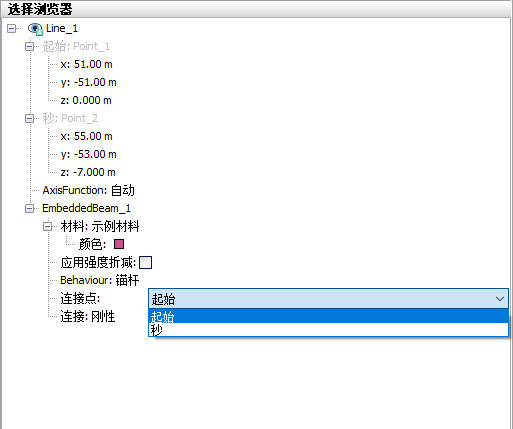
上图中用的是盗版软件，盗版软件的翻译估计就是直接机翻的，所以不用在意他实际显示了什么。这里面的First连接点指的是绘制这条线对象时指定的第一个点，即在使用line命令时传入方法中的第一个坐标；Second连接点指的是绘制这条线对象时指定的第二个坐标。

所谓的连接点可以类比于端承桩打入持力层的部分，作为结构求解的边界条件。而注浆体则没有显示连接点的选择，而且其必须连接在点对点锚杆上。此处由于笔者本身的水平受限，暂无法解释注浆体为什么不考虑端部的作用效应。

3.2.2连接点与不同节点重合时不同类型的连接形式的区别

在上一节的桩和锚杆力学对象中，对线对象指定了相应的连接点，每个连接点都有以下三种形式的节点类型：Free、Hinged、Rigid，如下图所示：

按照以上的定义，三种节点类型翻译过来应该分别是：自由节点、铰节点和刚节点。

由于embedded桩一般是插入土中，或与其他类型的结构相连接。不同的连接对象在力学表现上存在一定区别。

当节点与土体单元的计算节点重合时，分别对于三种类型节点：

1. 自由节点：能够相对于相邻土自由移动和旋转，通过指定的界面单元与土体相互作用；
2. 绞节点：必须随着土单元一起平移，但是可以自由转动
3. 刚节点：位移与旋转与所连接的土体单元相一致。

当桩节点与结构单元计算节点重合时，分别对于以下三种类型节点：

1. 自由节点：能够相对于相邻土体和结构自由移动和旋转，但是所连接的结构对象不能够相对于土体自由移动或转动；
2. 绞节点：节点的位移与所连接的结构一致，但可以绕连接点自由转动；
3. 刚节点：节点的位移和转动均与所连接的结构相一致。

参数与算法

一个完整的embedde桩材料对象包含以下参数：杨氏模量E、重度$\gamma$ 、梁类型、桩的直径、计算长度、瑞利波参数、侧摩阻力参数，横向阻力参数和界面刚度因数。具体建模参数及说明如下表所示：

属性名	描述	计算公式或取值方法
PredefinedBeamType	定义的桩类型	0：实心圆，1：圆管，2，矩形
BeamType	定义桩的截面类型	0：默认，1：自定义
Elasticity	定义材料的弹塑性性质	0：弹性，1：弹塑性
E	杨氏模量	单位：kM/${{\rm{m}}^2}$
w	重度$\gamma$	单位：kM/${{\rm{m}}^3}$
Diameter	直径，当PredefinedBeamType为实心圆或圆管类型时配置	单位：m
Thickness	厚度，当PredefinedBeamType为圆管时配置	单位：m
Width	宽度，当PredefinedBeamType为矩形时配置	单位：m
A	面积，当BeamType为预定义时，会自动计算，矩形按正方形计算	单位： ${m^2}$
Iyy	${I_3}$关于第三个方向轴的截面惯性矩	单位：${m^4}$
Izz	${I_2}$关于第二个方向轴的截面惯性矩	单位：${m^4}$
sigy	屈服应力，当Elasticity为弹塑性的时候	单位：kN/${m^2}$
SkinResistance	桩侧摩阻力与深度的关系	0：线性关系，1：深度表，2：土层相关
Tstart和Tend	SkinResistance为0时，${T_{start/end,\max }}$起点和重点的侧摩阻力	单位：kN/m
SkinResistanceTable	多线性轴向阻力。当SkinResistance为1时，一个列表，双数索引为深度，单数索引为大小。如[0, 0, 1, 1, 2, 3]表示0m相对顶端长度时，侧摩阻力为0kN/m，1m为1kN/m，2m为3kN/m	数组：单位分别是$m$和$kN/m$
Tmax	最大侧摩阻力	单位：kN/m
Fmax	最大桩端反力	单位：kN

其中，很多参数都是根据之前定义的桩截面形式来确定的，因此在配置embedded桩的相关参数时，应该配合GUI界面共同操作。

当PredefinedPileType配置为实心圆或圆管时，一定要注意，在输入直径和厚度之后，要算出面积A一起输入，这样惯性矩就会自动计算。如果只输入直径Diameter和厚度Thickness的话，Plaxis不会自动计算面积和惯性矩。

当PredefinedPileType配置为矩形时，如果BeamType为默认时，则会按照正方形计算面积与截面惯性矩；如果BeamType为自定义时，则会提示需要你手动输入面积和惯性矩。

圆形的截面惯性矩（以圆心为计算轴）计算公式如下所示：

$$ I = \frac{{\pi {D^4}}}{{64}} $$

圆管的截面惯性矩（以圆心为计算轴）计算公式如下所示：

$$ I = \frac{{\pi ({D^4} - {d^4})}}{{64}} $$

其中：D为直径或圆管外径，d为圆管内径。

正方形的截面惯性矩（平行于长度方向以1/2界面中心轴）计算公式如下所示：

$$ I = \frac{{{a^4}}}{{12}} $$

其中：a为正方形的边长。

其他类型截面的惯性矩计算公式可以参阅《材料力学》大学课本。

Plaxis2D和Plaxis3D中有关于embedded桩的材料属性文档及详情，详见：

• Plaxis2D-EmbeddedBeam2DMat
• Plaxis3D-EmbeddedBeam2DMat

Python接口及调用方法

使用Python创建embedded桩

与其他线单元相同，在创建embedded桩之前需要先创建线对象，然后基于线对象创建embedded桩。由于在Plaxis2D和Plaxis3D中，该实体单元均为线单元，因此在示例时不做两部分分别介绍。

首先在Plaxis中创建线对象，代码如下所示：

# Plaxis 2D中创建线对象
EmbeddedLine2D = g_i.line((30, -1), (40, -1))[-1]

# Plaxis 3D中创建线对象
EmbeddedLine3D = g_i.line((0, 0, -1), (1, 1, -1))[-1]

基于创建的线对象创建embedded桩对象：

# Plaxis 2D基于线创建embedded桩
Embedded2D = g_i.embeddedbeamrow(EmbeddedLine2D)

# Plaxis 3D基于线创建embedded桩
Embedded3D = g_i.embeddedbeam(EmbeddedLine3D)

Plaxis2D和3D中的构造方法有些区别，需要注意一下。

创建embedded桩的材料集：

# Plaxis 2D中创建embedded桩的材料集
Embedded2DMat = g_i.embeddedbeammat('MaterialName', '嵌固桩', 'Elasticity', 0, 'PredefinedBeamType', 0,
                                'BeamType', 0, 'E', 8E8, 'w', 20, 'Diameter', 1, 'SkinResistance', 0,
                                'Tstart', 300, 'Tend', 600, 'A', 0.785398163397448)
# Plaxis 3D中创建embedded桩的材料集
Embedded3DMat = g_i.embeddedbeammat('MaterialName', '嵌固桩', 'Elasticity', 0, 'PredefinedBeamType', 0,
                                'BeamType', 0, 'E', 8E8, 'w', 20, 'Diameter', 1, 'SkinResistance', 0,
                                'Tstart', 300, 'Tend', 600, 'A', 0.785398163397448)

将embedded桩的材料属性赋值成刚创建好的属性：

# Plaxis 2D中对材料赋值
Embedded2D.Material = Embedded2DMat
# Plaxis 3D中对材料赋值
Embedded3D.Material = Embedded3DMat

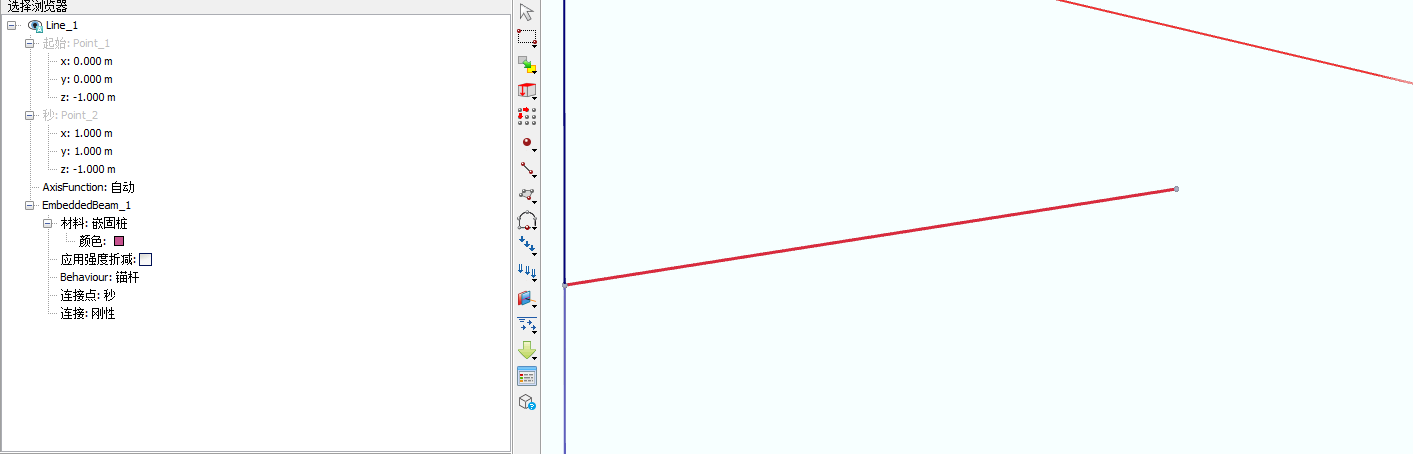
在上一节提到embedded桩需要配置力学行为，三个力学行为分别为：Pile、Rock bolt和Grout body。其中Pile和Rock bolt包含连接点属性，其中Pile的连接点属性分别为Top和Bottom；Rock bolt的连接点属性包括First和Second。下面演示将桩修改为锚杆，同时将连接点设置为Second。

# Plaxis 2D中修改embedded桩的力学行为
Embedded2D.Behaviour = 'Rock bolt'
Embedded2D.ConnectionPoint = 'Second'

# Plaxis 3D中修改embedded桩的力学行为
Embedded3D.Behaviour = 'Rock bolt'
Embedded3D.ConnectionPoint = 'Second'

修改好的结果如下图所示：

计算结果输出类型

完成结构计算之后，我们需要查阅输出的计算结果，embedded桩对象也不能直接在上面选取曲线点，而是有专门的输出对象ResultTypes.EmbeddedBeamRow（2D）和ResultTypes.EmbeddedBeam（3D）。Plaxis2D和Plaxis3D中的土工格栅输出对象的文档分别如下所示：

• Plaxis2D——ResultTypes.EmbeddedBeamRow
• Plaxis3D——ResultTypes.EmbeddedBeam

通过文档可以得embedded桩有很多类型的属性可以获取，通过调用getresults方法来得到计算结果。如需要获取embedded桩的每个节点的全部位移|u|，可以参考如下代码：

# 获取土工格栅上所有节点的总位移
g_o.getresults(Embedded2D, phase1, g_o.ResultTypes.Geogrid.Utot, 'node')

该方法接收4个传入参数：Embedded2D需要提取计算结果的embedded桩对象，phase1需要提取计算结果的计算阶段，g_o.ResultTypes.GeoEmbeddedBeamRowgrid.Utot需要获取的总位移结果类型，node指定获取实体单元上的节点计算结果，可选应力节点stress point。

获取embedded桩剪力的完整实例

下面展示一个在Plaxis 2D中获取一根埋入地下桩剪力分布的完整示例。 工程概况：一根直径为1m，长度为10m的桩竖直埋入预定的土中，桩顶正好与地面平齐，获取该桩的剪力分布值。

from plxscripting.easy import *
passwd = '**********************'
s_i, g_i = new_server('localhost', 10000, password=passwd)

s_i.new()
SMats = {}
SMats['砂土'] = g_i.soilmat('SoilModel', 4, 'gammaUnsat', 15, 'E50ref', 1E4, 'EurRef', 3E4,
                          'gammaSat', 15, 'DrainageType', 0, 'einit', 0.5, 'powerm', 0.7,
                          'cref', 0, 'phi', 31.6, 'psi', 1.6, 'EoedRef', 1E4, 'K0nc', 0.476,
                          'gamma07', 6e-05, 'G0ref', 5E4, 'MaterialName', '砂土')

g_i.gotosoil()
g_i.SoilContour.initializerectangular(-30, -80, 120, 50)
BH = g_i.borehole(-50)
BH.setproperties('Head', -50)
g_i.soillayer(50)
soilMat = SMats['砂土']
g_i.Soils[0].Material = soilMat

g_i.gotostructures()

EmbeddedLine2D = g_i.line((30, 0), (30, -10))[-1]
Embedded2D = g_i.embeddedbeamrow(EmbeddedLine2D)

Embedded2DMat = g_i.embeddedbeammat('MaterialName', '嵌固桩', 'Elasticity', 0, 'PredefinedBeamType', 0,
                                'BeamType', 0, 'E', 8E12, 'w', 20, 'Diameter', 1, 'SkinResistance', 0,
                                'Tstart', 300, 'Tend', 600, 'A', 0.785398163397448)

Embedded2D.Material = Embedded2DMat

g_i.gotomesh()
g_i.mesh(0.06, True)


g_i.gotostages()

phase1 = g_i.phase(g_i.Phases[0])
phase1.setproperties('Identification', '安装embedded桩', 'TimeInterval', 2)
# 激活所有的桩
g_i.activate(g_i.EmbeddedBeamRows, phase1)

g_i.calculate()

output = g_i.view(phase1)
s_o, g_o = new_server('localhost', output, password=passwd)

# 获取并输出桩的剪力大小
Q2D = list(g_o.getresults(Embedded2D, phase1, g_o.ResultTypes.EmbeddedBeamRow.Q2D, 'node'))
Y = list(g_o.getresults(Embedded2D, phase1, g_o.ResultTypes.EmbeddedBeamRow.Y, 'node'))
for y, q in zip(Y, Q2D):
    print(f'>>> 深度：{y}m，剪力{q}E-3kN/m')

>>> 深度：0m，剪力-0.000485517465992518E-3kN/m
>>> 深度：-0.625m，剪力-0.00507228975919785E-3kN/m
>>> 深度：-1.25m，剪力-0.0114775011042157E-3kN/m
>>> 深度：-1.875m，剪力-0.0187621274805758E-3kN/m
>>> 深度：-2.5m，剪力-0.0259871448678078E-3kN/m
>>> 深度：-2.5m，剪力-0.028356895774303E-3kN/m
>>> 深度：-3.125m，剪力-0.0342173025202201E-3kN/m
>>> 深度：-3.75m，剪力-0.0407684655873386E-3kN/m
>>> 深度：-4.375m，剪力-0.0463305452932266E-3kN/m
>>> 深度：-5m，剪力-0.0492237019554526E-3kN/m
>>> 深度：-5m，剪力-0.0194693617283525E-3kN/m
>>> 深度：-5.625m，剪力-0.0525675593713251E-3kN/m
>>> 深度：-6.25m，剪力-0.0462330319718316E-3kN/m
>>> 深度：-6.875m，剪力-0.0147502065462081E-3kN/m
>>> 深度：-7.5m，剪力0.0275964898892093E-3kN/m
>>> 深度：-7.5m，剪力0.0840522499891164E-3kN/m
>>> 深度：-8.125m，剪力0.0457888431901156E-3kN/m
>>> 深度：-8.75m，剪力0.0167846473837692E-3kN/m
>>> 深度：-9.375m，剪力0.0850803233854977E-3kN/m
>>> 深度：-10m，剪力0.338716532010722E-3kN/m

下一节

本节主要介绍了两类实体单元：土工格栅和embedded桩的相关参数特性和Python脚本的模型实现。下一节将介绍锚杆的特性与用法。

由于该教程是以笔者的知识水平为视角撰写的，因此难免存在各种疏漏与表述不清楚的部分，同时对于教程中所给的示例代码均假设读者具有一定的Python程序设计水平，因此部分简单的内容没有进行呈现。

希望读者们可以不吝赐教，在文章底部或通过其他方式提供一些改进的建议。