1引言

土压力：土体自重及其作用于土体上各种外力共同作用对挡土结构物产生的侧向压力，称为土压力。

挡土结构物：挡土结构物是防止土体坍塌失稳的结构物，最常见是各种形式的挡土墙。挡土结构物主要应用于防止土坡坍塌，主要结构类型一般包括：重力式挡墙、悬臂式挡墙、扶臂式挡土墙、锚杆式挡土墙和加筋式挡土墙等。

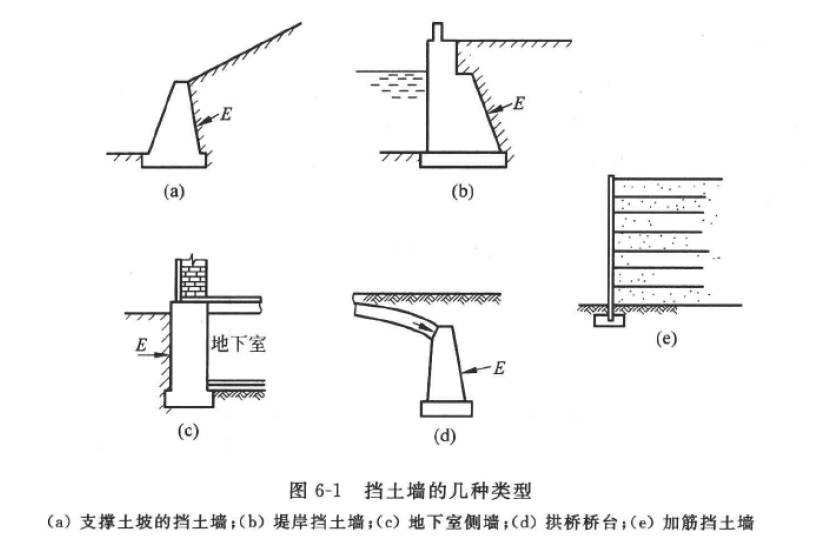
在进行挡土结构设计时，需要确定土压力的性质及土压力的大小、方向、分布和合力作用点。根据墙体的位移情况和墙后土体所处的应力状态，作用在挡土墙墙背上的土压力主要分为：

1. 静止土压力，墙体受到侧向土压力之后，墙身变形或位移很小默认墙不发生变形，土体处于弹性平衡状态，此时的挡土墙受到的土压力为静止土压力，一般用$E_0$表示；

2. 主动土压力，挡土墙受墙后填土作用而发生背离填土方向移动或沿墙趾的转动，使得墙后填土达到极限平衡状态、此时，土体对挡土墙墙背的压力称为主动土压力，一般用$E_a$表示；

3. 被动土压力，挡土墙在巨大的外力作用下，向填土方向移动或转动，使墙后填土受到墙体挤压。当墙后土体达到极限平衡状态时，作用在挡土墙上的土压力称为被动土压力，用$E_p$表示。

土压力的大小关系为：被动土压力 > 静止土压力 > 主动土压力，即$E_p > E_0 > E_a$

对于一般边坡来说，边坡的支挡结构除了受到土压力之外还会受到土沿软弱滑动面滑动的滑坡推力。若在土体或碎裂状或散体结构岩体中开挖低矮边坡时，主用于支挡结构上的主要荷载仍然是土压力；对于用抗滑桩、预应力锚索抗滑桩等支挡结构加固的高陡边坡，其主要荷载是部分坡体沿滑面所产生的的滑坡推力P。

本文主要针对低矮边坡，或一般工程基坑的支挡结构的的受力特性进行讨论，因此主要的讨论对象包括三类土压力的理论推导过程、计算方法、规范用法和当前研究进展等几个方面。

2土压力的经典理论

经典的土压力计算理论均假设土体为各向同性的均值半无限体，且在长度方向上处处相同，因此三维空间中的支护结构土压力计算模型可以简化为平面应变问题。

2.1静止土压力理论

静止土压力为当墙体静止不动，位移量为，转角为零情况下土体对结构物产生的土压力。一般用于修筑在坚硬岩石地基上、断面很大的挡土墙的土压力计算，此时挡土墙由于刚度和自重较大，假定为不发生位移，挡土墙后土体处于静止的弹性平衡状态。

平面问题下的静止土压力的计算模型如下图所示：

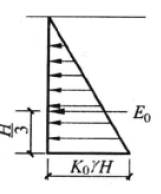
根据弹性半无限体的应力应变理论，深度处的竖向应力为土的自重应力$\gamma z$，由广义胡克定律：

$$ {\varepsilon _y} = \frac{{{\sigma _y}}}{E} - \frac{{\mu ({\sigma _x} - {\sigma _y})}}{E} $$

基于平面问题的基本假定和地面水平下各向同性半无限空间土体在竖直切面上不存在剪应力只产生竖向变形，推出： $ \varepsilon _x = \varepsilon _y = 0 $ 代入广义胡克定律公式可以得到： $ \sigma _x = \sigma _y = K_0\sigma _z $ 。其中 $ K _0 = \frac{\mu}{1-\mu} $ 。

其中：$\mu$为土体的泊松比，一般可以的取值为：

• 砂土：0.2~0.25
• 粘性土：0.25~0.4

一般$K_0$的取值在0.25~0.67之间，理想刚体$\mu = 0$，液体$\mu = 0.5$。Jaky^[1]在1944年通过大量的实验室实验研究了了黏土和粉土的静止土压力系数分布规律，拟合得到了一个估算土的静止土压力系数经验公式，如下所示：

$$\text{砂性土}: K_0 = 1 - sin(\varphi')$$ $$\text{粘性土}: K_0 = 0.95 - sin(\varphi')$$ $$\text{超固结土}: K_0 = \sqrt{OCR}(1 - sin(\varphi'))$$

其中：$\varphi’$为有效内摩擦角，$OCR$为超固结比。我国的《公路桥涵地基与基础设计规范》^[2]中给出了静止土压力系数的参考值，如下表所示：

土名	砾石、卵石	砂土	粉土	粉质黏土	黏土
$K_0$	0.20	0.25	0.35	0.45	0.55

2.2朗肯土压力理论

当前工程上实际应用最多的经典土压力理论，其基本原理仍基于半无限土体计算模型。并基于以下3种假设：

1. 挡土墙墙背垂直、光滑；
2. 挡土墙墙后填土表面水平，土质均匀；
3. 墙背处各点均处于极限平衡状态

这里的墙背处各点均处于极限平衡状态指的是主动土压力或被动土压力在当前的位移状态下达到稳定，即继续增加挡土结构的位移，土压力将不再增大。

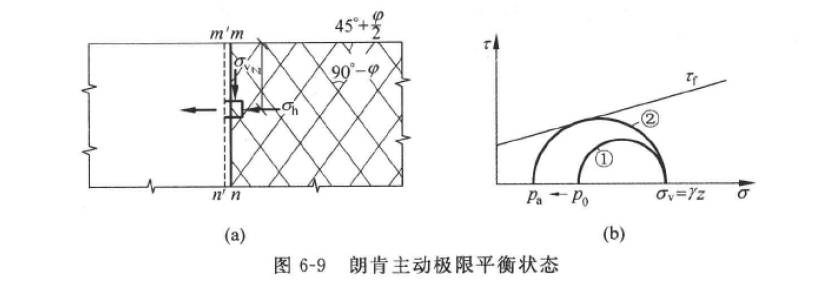
朗肯土压力的计算模型如下图所示：

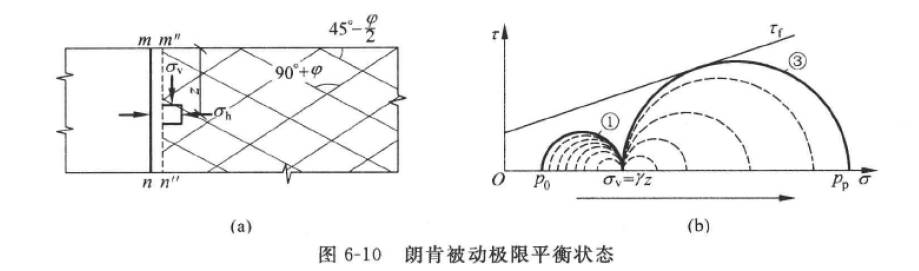
如上图所示(a)所示，当土体静止不动时，此时挡土墙收到的土压力为静止土压力，公式如上面静止土压力的所示。

当刚性挡墙面平行向外移动时，假定这个移动不会导致地面产生较大沉降，因此土的自重应力不变，而水平向应力由于颗粒间的摩擦和粘滞力的存在，会随着墙体位移的增大而减小。当垂直应力不变时水平向应力减少时，土的应力莫尔圆会向左边拓展，如上图的(b)所示。直到圆与破坏线相切，此时土体达到极限状态。对土单元进行受力分析，土的自重、土的滑裂面面剪应力和墙施加给土的反力达到平衡。

由于整个过程中土的水平应力在不断减小，竖直向应力不变，且土体单元的剪应力水平不断增加。因此土体单元的应力莫尔圆的大主应力不变，圆的半径不断增大，最终与破坏线相切。根据第四强度理论，土体单元与破坏线相切时达到即将破坏状态，将此状态做为极限状态。

此时根据土体单元的应力莫尔圆与破坏线的相对位置即可得到土体的应力状态，土体的自重应力已知，剪应力已知，可以计算出水平向应力，即主动土压力。

同理，朗肯被动土压力正好与之相反，随着墙体的位移增大，土体的水平应力不断增加，剪应力不断增大，应力莫尔圆的短边向右移动，如被动土压力计算模型图b所示。

基于以上，朗肯土压力的理论计算公式如下所示：

无粘性土：

主动土压力：

$$ {P_a} = {K_a}\gamma z = \gamma z{\tan ^2}(45^\circ - \frac{\varphi }{2}) $$

被动土压力：

$$ {P_p} = {K_p}\gamma z = \gamma z{\tan ^2}(45^\circ + \frac{\varphi }{2}) $$

其中：$\gamma$为土体的重度，地下水位以下使用有效重度；z为计算深度；$\varphi$为填土的内摩擦角。

有粘性土：

主动土压力：

$$ {P_a} = {K_a}\gamma z - 2c\sqrt {{K_a}} = \gamma z{\tan ^2}(45^\circ - \frac{\varphi }{2}) - 2c\tan (45^\circ - \frac{\varphi }{2}) $$

被动土压力

$$ {P_p} = {K_p}\gamma z + 2c\sqrt {{K_p}} = \gamma z{\tan ^2}(45^\circ + \frac{\varphi }{2}) + 2c\tan (45^\circ + \frac{\varphi }{2}) $$

对于朗肯土压力的假设一来说，很多情况墙背侧存在墙背不垂直的情况。基于应力莫尔圆理论，将墙土间的相互作用力角度调整为垂直于墙面的方向，根据平衡条件重新进行计算，得到：

无粘性土主动土压力：

$$ {P_a} = \gamma z\cos \beta \frac{{\cos \beta - \sqrt {co{s^2}\beta - {{\cos }^2}\varphi } }}{{\cos \beta - \sqrt {co{s^2}\beta - {{\cos }^2}\varphi } }} $$

无粘性土被动土压力：

$$ {P_a} = \gamma z\cos \beta \frac{{\cos \beta + \sqrt {co{s^2}\beta - {{\cos }^2}\varphi } }}{{\cos \beta - \sqrt {co{s^2}\beta - {{\cos }^2}\varphi } }} $$

2.3库伦土压力理论

库伦土压力表达式较为复杂，但是其解决了朗肯土压力的一些假设条件，使得更加接近实际工程。库伦土压力主要基于以下基本假设：

1. 挡土墙是刚性的；
2. 挡土墙后填土为无粘性土；
3. 当挡土墙向前或向后偏移时，墙后滑动土楔体沿墙背和某个通过墙踵的平面发生滑动；
4. 滑动土楔体视为刚体，并处于极限平衡状态；

库伦土压力理论与朗肯土压力理论最大的区别在于研究对象的不同，库伦土压力的研究对象是滑动土楔体，这是宏观上的滑动土层实体；朗肯土压力研究的对象为土体单元，其基本理论的推导来自于第四强度理论。

库伦土压力的计算模型如下图所示：

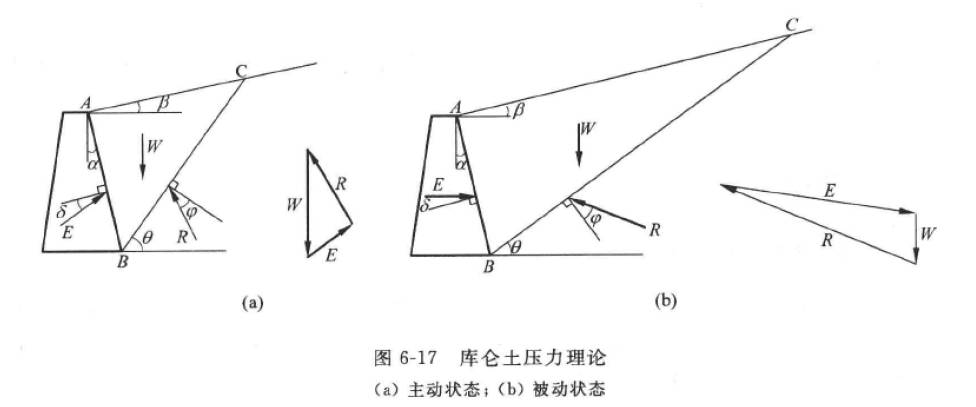
从计算示意图可以得到，计算模型不再要求挡土墙竖直且光滑，同时也不再要求墙后土体表面水平。分别设墙后挡土面与垂直方向的夹角为$\alpha$；墙后填土表面与水平面的夹角为$\beta$；滑动土楔的重力为W；挡墙与土的摩擦角为$\delta$；滑动面与水平方向的夹角为$\theta$。

由于挡土墙向外偏移，土楔体存在向外滑动的趋势，因此下层土体传递的反力在滑裂面发现方向下方，斜向上。

结合以上假定和定义，库伦滑动土楔体应该满足水平和竖直方向上的受力平衡，力矩平衡条件。首先定义墙和土的约束反力为$E$，滑动土楔的自重为$W$，滑裂面一下的土对土楔体滑动的约束反力为$R$，构造力的平衡三角形。如下图所示：

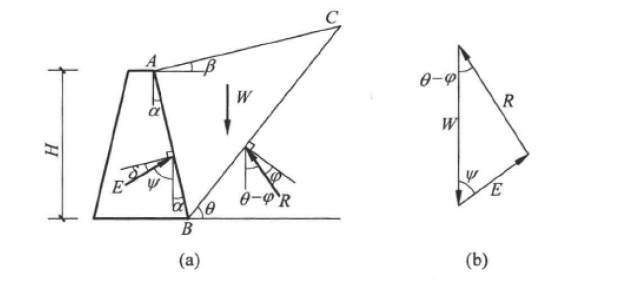
基于余弦定理有：

$$ \frac{E}{{\sin (\theta - \varphi )}} = \frac{W}{{\sin (180^\circ - (\theta - \varphi + \psi ))}} $$

基于解析几何得到，土楔体的重量计算表达式如下式所示：

$$ W = \frac{{\gamma {H^2}}}{2} \times \frac{{\cos (\alpha - \beta )\cos (\theta - \alpha )}}{{{{\cos }^2}(\alpha )\sin (\theta - \alpha )}} $$

由于滑动面与水平方向的夹角不确定，因此将滑动面与水平方向的夹角作为自变量，考虑在当前表达式下的土压力的极大值，将其作为库仑理论下的主动土压力。即$\frac = 0$当时，E的取值作为主动土压力值。计算表达式如下所示：

$$ E = \frac{1}{2}\gamma {H^2}{K_a} $$

其中：

$$ {K_a} = \frac{{{{\cos }^2}(\varphi - \alpha )}}{{{{\cos }^2}\alpha \cos (\alpha + \delta )(1 + \sqrt {\frac{{\sin (\varphi + \delta )\sin (\alpha - \beta )}}{{\cos (\alpha + \delta )\cos (\alpha - \beta )}}} )}} $$

其中：$\delta$墙土摩擦角可以由实验确定，一般取为$(\frac{1}{3}\sim\frac{2}{3})\varphi $，对于不同的墙土接触情况，相关研究对墙土情况做了分类和推荐，如下表所示：

挡土墙情况	外摩擦角$\delta$	挡土墙情况	外摩擦角$\delta$
墙背平滑、排水不良	(0-0.33)$\varphi$	墙背很粗糙、排水良好	(0.5-0.67)$\varphi$
墙背粗糙、排水不良	(0.33-0.5)$\varphi$	墙背与填土间不能滑动	(0.67-1.0)$\varPhi$

当墙背垂直、光滑和填土面水平时，库伦主动土压力计算公式将退化为朗肯土压力计算公式。

对于无粘性土的被动土压力计算原理与主动土压力相同，主要区别在于下层土在土楔体上提供的反力的方向，其在滑裂面发现方向的上方。计算模型如下图所示：

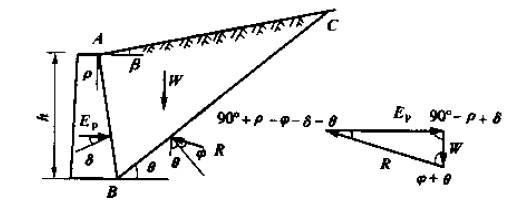
用库伦理论推导被动土压力计算公式时，正弦定律改写为：

$$ E = W\frac{{\sin (\theta + \varphi )}}{{\sin (\theta + \varphi + \psi )}} $$

被动土压力系数则变为：

$$ {K_a} = \frac{{{{\cos }^2}(\varphi + \alpha )}}{{{{\cos }^2}\alpha \cos (\alpha - \delta )[1 + \sqrt {\frac{{\sin (\varphi + \delta )\sin (\alpha + \beta )}}{{\cos (\alpha - \beta )\cos (\alpha - \beta )}}} ]}} $$

对于库伦土压力算法的求导规则，当主动土压力的大小达到极大值时，$\theta = 45^\circ - \frac{\varphi }{2}$；当被动土压力达到最大值时，$\theta = 45^\circ + \frac{\varphi }{2}$

库伦主动土压力计算公式适用条件：

1. 墙背土为无粘性土；
2. 滑裂面正好为经过墙踵的平面；
3. 墙后土层表面倾角小于土的内摩擦角；
4. 墙体与土接触一侧倾斜角较小时：
   1. 当墙背向外倾斜过大时假定土楔体破裂面为平面会使计算得到的土压力减小到0；
   2. 当墙背向内倾斜过大时滑动土体可能沿第二破裂面滑动。

3特殊情况下的土压力计算方法

3.1多层土层时的土压力计算方法

多层土时的土压力计算方法基于库伦土压力理论计算法，当墙后土体有多层土体时，第一层按照均质土套用库伦土压力计算方法进行计算。

而第一层以下的土层时，可以按土层以上超载的情况套用库伦土压力模型计算当前土层的土压力。计算公式如下所示：

$$ p_a = (\gamma_1 H1 + \gamma_2 * z) K_{a2} $$

$$ {E_{a2}} = ({\gamma _1}{H_{_1}}{H_2} + \frac{{{\gamma _2}H_2^2}}{2}){K_{a2}} $$

其中，$K_{a2}$为第二层土层的主动土压力系数。土压力大小示意图如下图所示：

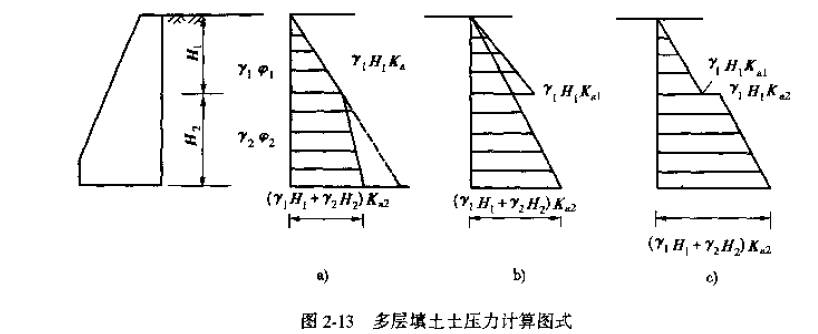
3.2有限土体的土压力计算

实际工程中，若开挖基坑在城市中，四周都是建筑物基础或其他加强地基，或边坡支护土坡后的宽度有限使得不满足半无限空间体假定。区分有限土体和无限土体的主要原则为通过墙踵的滑裂面是否能够向上延伸至土体表面。如果墙后填土中存在固定障碍物阻碍了滑裂面直线的发展，那么墙后土体应当作为有限土体考虑，如下图所示：

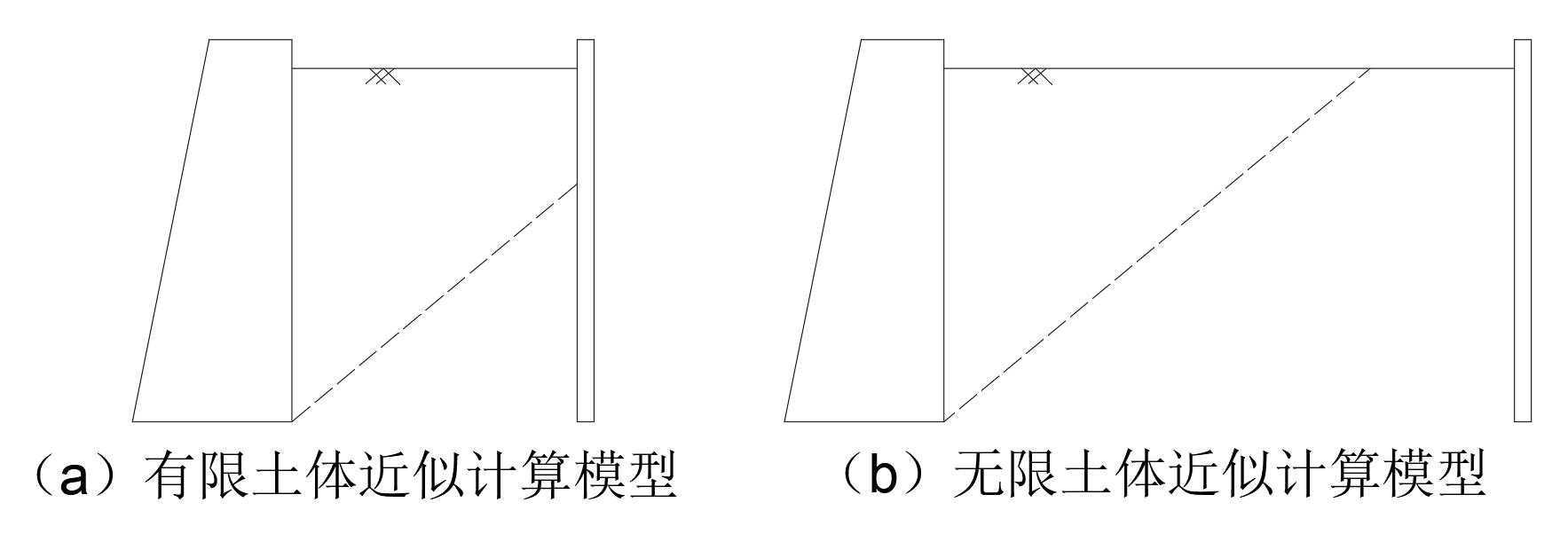
3.2.1有限土体的主动土压力

有学者针对有限土体的主动土压力算法进行了研究^[3]，此时计算模型如下图所示：

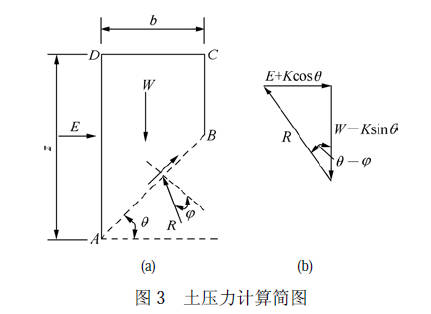
基于库伦土压力的计算方法，土体重力的表达式变为：

$$ W = \gamma b(z - \frac{b}{2}\tan \theta ) $$

该计算模型考虑了粘结力K，其计算表达式如下式所示：

$$ K = \frac{b}{{\cos \theta }}c $$

基于正弦定理，推导有限状态下的土压力计算表达式为：

$$ E = [\gamma b(z - \frac{b}{2}\tan \theta ) - bc\tan \theta ]\tan (\theta - \varphi ) - bc $$

当 $\frac{{dE}}{{d\theta }} = 0$ ，此时$\theta$等于：

$$ \theta ' = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{2\gamma b\tan \varphi + 2c\tan \varphi }}[ - 2\gamma b}\\ { - 4c + 2({\gamma ^2}{b^2} + 4\gamma bc + 4{c^2} + 2{\gamma ^2}bz{{\tan }^3}\varphi }\\ { + 2{\gamma ^2}bz\tan \varphi + {\gamma ^2}{b^2}{{\tan }^2}\varphi + 4\gamma bc{{\tan }^2}\varphi }\\ { + 4\gamma zc{{\tan }^3}\varphi + 4\gamma zc\tan \varphi + 4{c^2}{{\tan }^2}\varphi {)^{\frac{1}{2}}}]} \end{array}} \right\} $$

此时的主动极限状态下的滑裂面倾角不再是一个常数，与土体的物理力学性质、有限土体宽度和墙踵计算深度有关。根据计算结果来看，有限土体的主动土压力的大小较朗肯土压力理论计算得到的土压力更小，因此应用朗肯或库伦土压力计算有限土体的土压力在安全上是可行的。

3.2.2有限土体的被动土压力

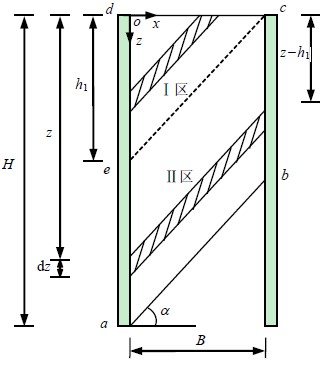
一些学者对有限宽度下的被动土压力展开了研究^[4][5]，其中徐日庆老师在库伦理论的基础上对被动土压力计算表达式做了进一步分析，计算模型如下图所示：

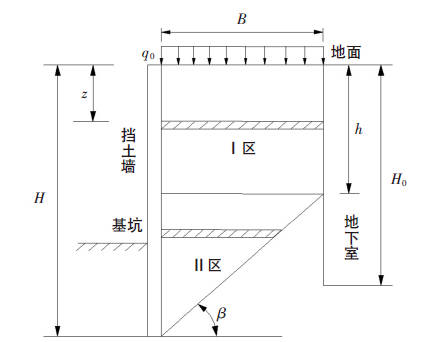
图中Ⅰ区为梯形滑动土楔体，墙后土体在墙体位移的推挤过程中会产生土工效应，因此不能直接套用库伦土压力滑动土楔的平衡模型。对Ⅰ区进行分析，该区域土体的大主应力轨迹线如下图所示：

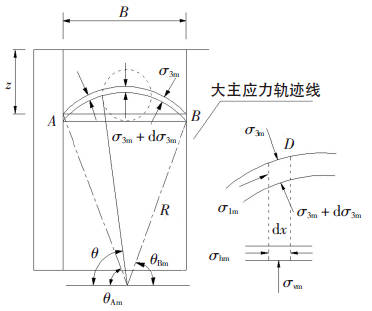
考虑土拱效应，基于朗肯土压力的分析方法绘制应力莫尔圆，墙后土体单元的应力状态如下图所示：

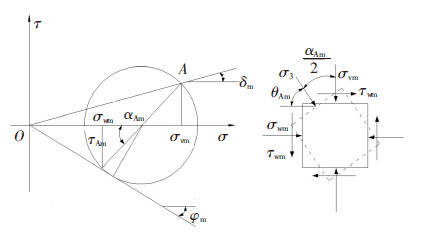
基于以上，推到得到Ⅰ区土体的被动土压力计算公式如下式所示：

$$ \begin{array}{*{20}{l}} {{K_{pw1}}{\rm{ = }}\frac{{{\sigma _{wm}}}}{{{{\bar \sigma }_{vm}}}} = }\\ {\frac{{3(\cos {\theta _{Am}} + \cos {\theta _{Bm}})({{\cos }^2}{\theta _{Am}} + {K_{pm}}{{\sin }^2}{\theta _{Am}})}}{{3(\cos {\theta _{Am}} + \cos {\theta _{Bm}}) + ({K_{pm}} - 1)({{\cos }^3}{\theta _{Am}} + {{\cos }^3}{\theta _{Bm}})}}} \end{array} $$

其中：$\theta{Am}$和$\theta{Bm}$分别为有限土体两侧的主应力偏转角，表示土体单元在土拱上的位置，计算公式如下式所示：

$$ \left\{ {\begin{array}{*{20}{c}} {{\theta _{Am}} = \frac{\pi }{2} - \frac{1}{2}[\arcsin (\frac{{\sin {\delta _m}}}{{\sin {\varphi _m}}}) + {\delta _m}]}\\ {{\theta _{Bm}} = \frac{\pi }{2} - \frac{1}{2}[\arcsin (\frac{{\sin {\alpha _m}}}{{\sin {\varphi _m}}}) + {\alpha _m}]} \end{array}} \right. $$

其中，$\delta_m$为外摩擦角的发挥值，$\varphi_m$为内摩擦角的发挥值，$\alpha_m$为梯形短边侧的外摩擦角发挥值。

3.3地震作用下的土压力计算

相关规范^[6]中未指出地震作用下的土压力计算方法，实际工程设计中一般使用拟静力法进行计算，忽略了地震波的动力效应^[7]。

拟静力法的实质是将复杂的动力下的地震土压力问题在静土压力理论的基础上进行修正从而转化为静力学问题，用静力下强度理论与本构模型进行计算。其将地震荷载作用看成一个简单的惯性力作用，忽略周期变化的特点。该计算方法基于以下基本假设：

1. 地震荷载简化为简单惯性力作用；
2. 墙后填土为刚体；
3. 土体内部处处均匀，各向同性。

对于地震波来说，地震波主要分为横波和纵波，我们对建构筑物进行设计的时候，一般对竖向承载力进行设计，因此地震作用下的水平横向力对建构筑物的危害很大，因此主要考虑地震的水平作用影响。 基于库伦土压力计算公式，将该惯性力等效为水平地震力P，作用于土楔体的重心，大小计算公式如下所示：

$$ P = C_z * k_H * G $$

其中：$C_z$为综合影响因素，表示结构体系的地震反应与理论计算的差异；$k_H$为水平地震系数，g为地震时地面最大水平加速度的统计平均值与重力加速度的比值；G为破裂土楔体自重力。$k_H$的推荐取值如下表所示：

地震动峰值加速度	0.1g~0.15g	0.2g~0.3g	>=0.4g
水平地震系数$k_H$	0.1	0.2	0.4

地震力P的方向水平并指向墙后土体滑动的方向，将其作为滑动土楔体收到的外力，带入到库伦土压力的计算模型中，如下图所示：

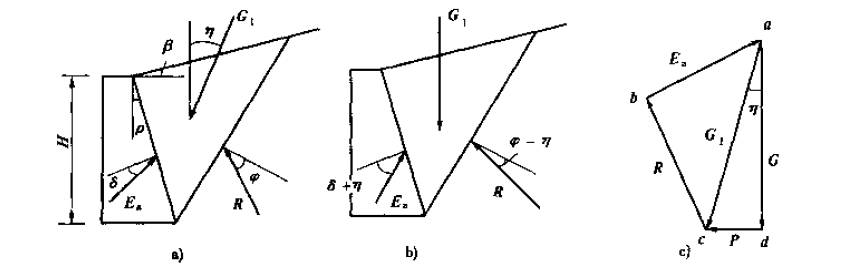
库伦主动土压力的计算公式如下式所示：

$$ {E_a} = \frac{1}{2}\frac{\gamma }{{\cos \eta }}{H^2}{K_a} $$

其中：$\eta$为土楔体重力和地震力合力与竖直方向的夹角。

3.4墙后土体有水时的土压力计算方法

墙后填土土体浸水时，一方面因水的浮力作用使土的自重减小；另一方面，浸水时砂性土的抗剪强度的变化虽不大，但粘性土的抗剪强度会发生显著的降低。因此，在上压力计算中必须考虑土体浸水的影响。此外，当墙后土体中出现水的渗流时，还应计入动水压力的影响。

规范^[6]中定义了两种计算方式：水土合算和水土分算。

$$ {p_{ak}} = {\sigma _{ak}}{K_{a,i}} - 2{c_i}\sqrt {{K_{a,i}}} $$

$$ {K_{a,i}} = {\tan ^2}(45 - \frac{{{\varphi _i}}}{2}) $$

$$ {p_{pk}} = {\sigma _{pk}}{K_{p,i}} - 2{c_i}\sqrt {{K_{p,i}}} $$

$$ {K_{p,i}} = {\tan ^2}(45 + \frac{{{\varphi _i}}}{2}) $$

式中：$p{ak}$为支护结构外侧，第层土中计算点的主动土压力强度标准值($k{pa}$)；当$p{ak}<0$时，应取$p{ak}=0$；$\sigma{ak}$,$\sigma{pk}$分别为支护结构外侧、内侧计算点的土中竖向应力标准值(kPa)；$K{a,i}$,$K{p,i}$分别为第i层土的主动土压力系数、被动土压力系数；$ci$,$\varphi_i$第i层土的粘聚力(kPa)、内摩擦角(°)；$p{pk}$──支护结构内侧，第i层土中计算点的被动土压力强度标准值(kPa)。

对于水土分算土层土压力计算公式如下：

$$ {p_{ak}} = ({\sigma _{ak}} - {u_a}){K_{a,i}} - 2{c_i}\sqrt {{K_{a,i}}} + {u_a} $$

$$ {p_{pk}} = ({\sigma _{pk}} - {u_p}){K_{p,i}} + 2{c_i}\sqrt {{K_{p,i}}} + {u_p} $$

其中：$U_a$,$U_p$分别为支护结构外侧、内侧计算点的水压力(kPa)。综合以上水土分算和合算使用条件，应用以上计算表达式导出基坑围护结构土压力计算模型如下图所示：

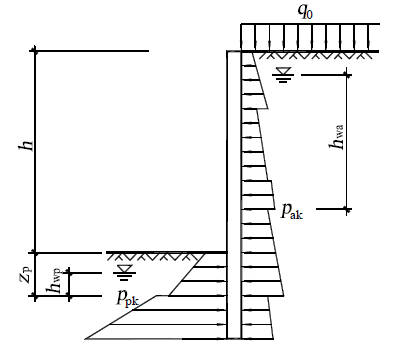
在支护结构土压力的影响范围内，存在相邻建筑物地下墙体等稳定的刚性界面时，可采用库仑土压力理论计算界面内有限滑动楔体产生的主动土压力，此时，同一土层的土压力可采用沿深度线性分布形式。

4非极限状态下的土压力计算方法

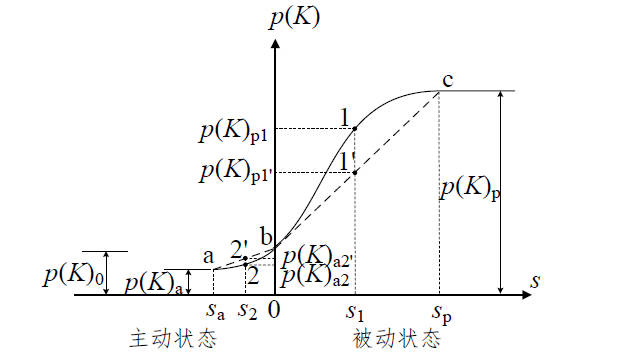
已有的理论计算方法均是假定土体位移已经达到极限状态。在实际工程中，主动土压力的位移极限状态较为容易达到，被动土压力的位移极限状态由于需要较大的土体位移，往往超过工程允许范围。因此有不少研究者针对土体位移未达到极限状态时的土压力理论进行了相关研究^[8][9][10]，当前常用的土体位移修正示意图如下图所示：

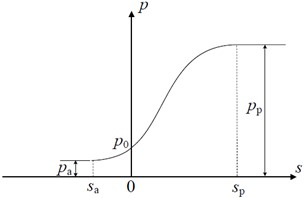
但非极限状态下的主被动土压力较为精确的计算方法至今仍未有确定的结论，相关的研究均假设挡土结构的变形特性后探究土压力的变化规律。

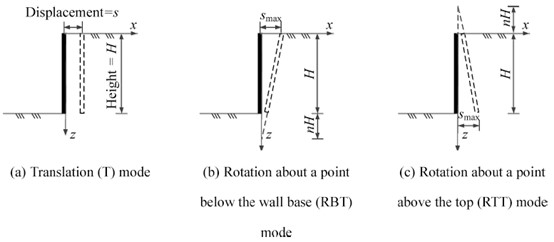
基坑支护结构在土压力，支撑力等综合作用下会发生一定的位移。要研究挡土墙在非极限状态下的土压力计算方法，必须要明确挡墙的变形特性。当前的研究针对支护结构的变位模式将支护结构的变形分为平动模式（T模式）、绕顶部转动模式（RT模式）、绕底部转动模式（RB模式）。

张恒志等^[13]基于静力平衡方法结合离散元模拟等方法分析了RB模式下的主动土压力分布问题，假定了墙后土体的滑裂线倾角与库伦理论一致，推导了RB模式下有限土体主动土压力的理论计算公式。Fan等^[12]通过假定被动土压力系数与位移呈线性关系，在库伦土压力理论的基础上对被动极限状态下的土压力系数进行了修正，使土压力模型能适应不同的墙体运动，推导了墙体分别在T模式、RT模式、RTT模式、RB模式、RBT模式下的被动土压力系数的计算公式，结合了模型实验得到的实验数据，验证了推导的理论公式的可行性。分别对于以上几种模式总结现有研究提出的主动土压力计算公式和被动土压力计算公式。

4.1RB模式下的土压力计算方法

RB模式下的主动土压力计算公式：

$$ {p_h} = \left\{ {\begin{array}{*{20}{c}} {{K_1}\gamma z(0 \le z \le {h_1})}\\ {{K_2}\gamma (z - {h_1}) + {K_1}\gamma {h_1}({h_1} < z \le H)} \end{array}} \right. $$

其中：$K_1$为滑裂面分割线I区三角形计算区域同时也是库伦理论中的主动土压力系数，$K_2$为滑裂面分割线Ⅱ区计算区域的主动土压力系数，$h_1$为滑裂面分割线在支护结构上的高度。

$$ {K_1} = \frac{{\sin (\alpha - \varphi )\cos \delta \cot \alpha }}{{\cos (\alpha - \varphi - \varphi )}} $$

$$ {K_2} = \frac{{\cos (\alpha - \varphi + \delta )}}{{\cos (\alpha - \varphi - \delta )}}{K_1} $$

$${h_1} = B\tan \alpha$$

其中：$\alpha_{cr}$为库伦主动土压力滑裂面倾角，计算公式为：

$$ {\alpha _{cr}} = \arctan \left[ {\sqrt {\frac{{\tan \varphi }}{{\tan (\varphi + \delta )}} + {{\tan }^2}(\varphi ) + \tan (\varphi )} } \right] $$

主动土压力的计算模型如下图所示：

RB模式下的被动土压力计算公式为^[13]：

$$ {p_{RB}} = ({K_p} - {K_0})\gamma \left( {\frac{3}{{2 - 3m}}\frac{{{z^2}}}{H} - \frac{{3m}}{{2 - 3m}}z} \right) + {K_0}\gamma z $$

其中：$K_p$被动极限状态下的库伦土压力系数；$K_0$为静土压力系数，m=x/H为旋转中心的参数。

$$ {K_p} = \frac{{{{\cos }^2}\varphi }}{{{{(\sqrt {\cos \delta } - \sqrt {\sin (\delta + \varphi )\sin \varphi } )}^2}}} $$

4.2T变位模式下的土压力计算方法

T模式下的未达到极限状态和极限状态的被动土压力的计算公式：

$$ {p_T} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\left( {{K_p} - K_0} \right)\frac{s}{{{s_p}}} + {K_0}} \right]\gamma z}&{s \le {s_p}}\\ {{K_p}\gamma z}&{s > {s_p}} \end{array}} \right. $$

其中：$K_p$为被动极限状态下的库伦土压力系数；$K_0$为静土压力系数；s为土体位移大小；$s_p$为主动土压力极限位移大小。

RBT模式下的被动土压力计算公式如下式所示：

$$ {p_{RBT}} = \left\{ {\begin{array}{*{20}{c}} {{K_p}\gamma z}&{0 \le z \le (1 - \frac{{{s_p}}}{{{s_{\max }}}})H}\\ {\left( {{K_0} - ({K_0} - K{'_p})\frac{{{s_{\max }}}}{{{s_p}}}\frac{{H - z}}{H}} \right)\gamma z}&{(1 - \frac{{{s_p}}}{{{s_{\max }}}})H \le z \le H} \end{array}} \right. $$

其中：$K{‘p}$为RBT模式下的修正土压力系数；${s{\max }}$为支护结构的最大位移大小。

$$ K{'_p} = - \frac{2}{{1 + 3n}}{K_0} + \frac{{3 + 3n}}{{1 + 3n}}{K_p} $$

其中：n为插入深度比。

RTT模式下的被动土压力计算公式如下式所示^[13]：

$$ {p_{RTT}} = \left\{ {\begin{array}{*{20}{c}} {(K{'_p} - {K_0})\frac{{z + nH}}{{(n + 1)H}}\frac{{{s_{\max }}}}{{{s_p}}}\gamma z + {K_0}\gamma z}&{{s_{\max }} \le {s_p}}\\ {\begin{array}{*{20}{c}} {\left( {{K_0} - ({K_0} - K{'_p})\frac{{{s_{\max }}}}{{{s_p}}}\frac{{z + nH}}{{(n + 1)H}}} \right)\gamma z}&{0 \le z \le (n + 1)\frac{{{s_p}}}{{{s_{\max }}}}H - nH}\\ {{K_p}\gamma z}&{(n + 1)\frac{{{s_p}}}{{{s_{\max }}}}H - nH \le z \le H} \end{array}}&{{s_{\max }} > {s_p}} \end{array}} \right. $$

以上主动土压力计算模型如下图所示：

4.3其他变位模式下的挡土结构线性变形土压力计算理论

本课题组的的范晓真师姐^[11][12]基于库伦土压力计算理论提出了土压力的线性计算理论，其基于以下基本假设：

1. 挡土墙刚性，只能绕某一点旋转，不会应为土压力变化产生扰度
2. 主动土压力和被动土压力与墙体位移的关系为线性关系

刚性支护结构的力学计算模型如下图所示：

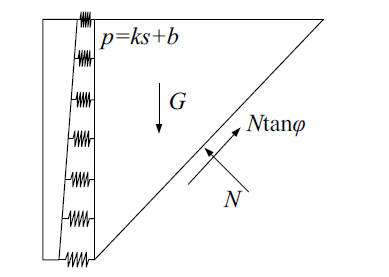
师姐对提出的考虑支护结构变形和变位模式的非极限土压力计算方法进行验证与分析，分别将提出的计算方法与不同支护结构变位模式（T 模式、RB 模式、RBT 模式、RT 模式以及 RTT 模式）下的主动土压力和被动土压力的试验结果进行对比，论证了该土压力的线性计算理论可以进一步对基于变形控制的非对称开挖基坑进行整体受力分析与计算中，并给出了算例。

5参考文献

1. JAKY I. The coefficient of earth pressure at rest [J]. Journal Soc of Hungarian Architects & Engineers, 1944 ↩
2. 公路桥涵设计通用规范[M]. 交通行业标准. 2015: 80p:A4. ↩
3. 马平, 秦四清, 钱海涛. 有限土体主动土压力计算 [J]. 岩石力学与工程学报, 2008, S1): 3070-4. ↩
4. 徐日庆, 徐叶斌. 考虑剪应力作用的有限土体被动土压力分析 [J]. 湖南大学学报(自然科学版), 2020, 47(09): 76-84. ↩
5. 应宏伟, 张金红, 王小刚, et al. 有限土体刚性挡墙平动模式被动土压力试验研究 [J]. 岩土工程学报, 2016, 38(06): 978-86. ↩
6. 中国建筑科学研究院, 中冶建筑研究总院有限公司, 华东建筑设计研究院有限公司, et al. 建筑基坑支护技术规程 [M]. 行业标准-建筑工业. 2012: 220P.;B5. ↩
7. 汪刘军, 邓亚虹, 孙科, et al. 挡土墙地震土压力计算方法研究综述 [J]. 煤炭科学技术, 2018, ↩
8. CONTE E, TRONCONE A, VENA M. A method for the design of embedded cantilever retaining walls under static and seismic loading [J]. Geotechnique, 2017, 67(12): 1081-9. ↩
9. LIU, H. Required reinforcement stiffness for vertical geosynthetic-reinforced-soil walls at strength limit state [J]. Geotechnique, 2016, ↩
10. MING-XI O U, LIU X R, SHI J X. Earth pressure applied in retaining wall of deep foundation pit considering influence of unloading and deformation [J]. Journal of Central South University(Science and Technology), 2012, 43(2): 669-74. ↩
11. 范晓真. 非对称开挖内撑式支护受力变形机理及变形控制设计理论 [D]; 浙江大学, 2021. ↩
12. FAN X-Z, XU C-J, LIANG L-J, et al. Analytical solution for displacement-dependent passive earth pressure on rigid walls with various wall movements in cohesionless soil [J]. Computers and Geotechnics, 2021, 140(104470. ↩
13. 张恒志, 徐长节, 梁禄钜, et al. RB 模式下刚性挡墙有限土体主动土压力的 离散元模拟与理论研究 [J]. 岩土力学, 42(10): 2895-907. ↩