题目

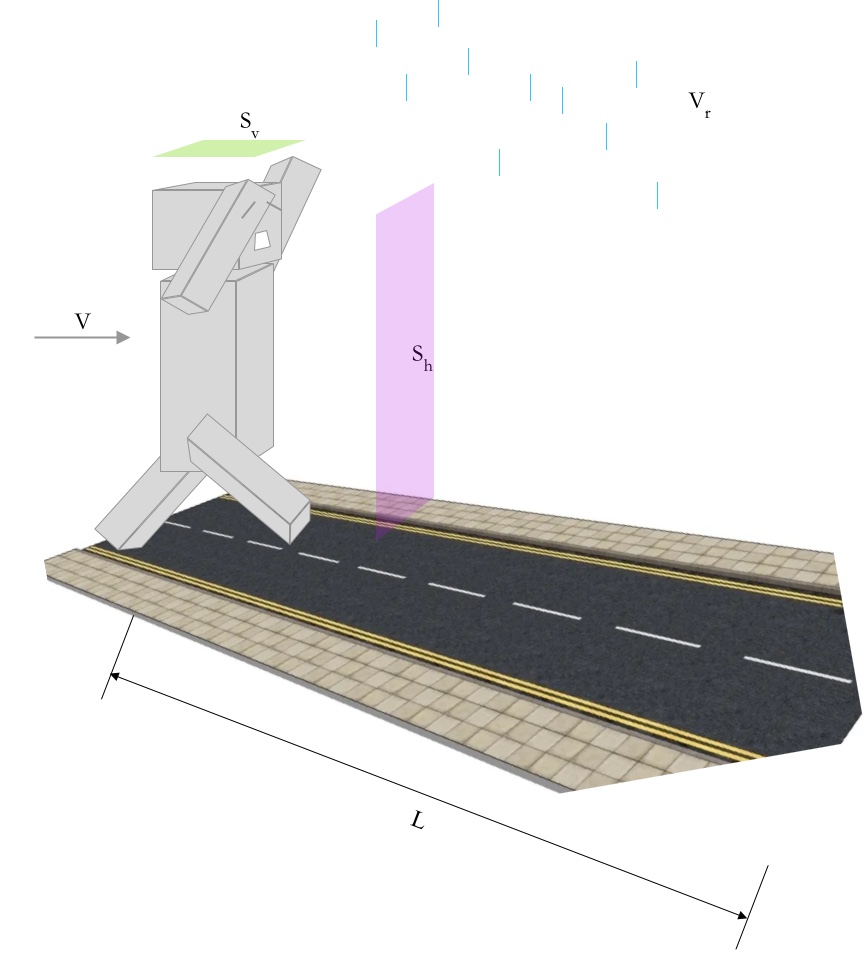
如图所示：无风时，雨以速度Vr垂直落下，行人用速度V步行距离L回家。现在已知他的前部面积为Sh，顶部面积为Sv，假定单位时间内雨水打湿的面积占物体表面积的百分比为n，试求：

1. 行人身体表面将淋多少雨？

2. 行人应该用多大速度回家才能淋最少的雨？

3. 假如奔跑方向有风，风速为Vw，此时应以多大速度奔跑？

4. 请设计合理的方法来测定雨的下落速度、雨水打湿面积百分比、人的正投影面积和侧投影面积，并给出各类天气下不同距离的奔跑速度建议。

题解

1问题重述

一个人在雨中奔跑，人的受雨面简化为水平和垂直的两个平面，已知雨水相对于地面运动的绝对速度和人相对于地面运动的绝对速度，完成以下任务： 1. 计算人在雨中奔跑的受雨量； 2. 人的运动速度与受雨量的关系模型； 3. 在雨有水平速度的情况下受雨量的关系模型； 4. 测定雨的下落速度的方法、雨水打湿的面积百分比，人的正投影和侧投影面积测算方法； 5. 不同天气下的奔跑建议。

2模型假设

为分析淋雨量与人奔跑速度的关系，定义如下假设： 1. 人在出发与到达目的地过程中始终保持匀速直线运动； 2. 下雨过程中每一滴雨水均以预定的v做匀速直线运动； 3. 所有雨滴的大小相同，雨滴的数量在时间上和空间上是分布均匀的。

3模型建立与求解

3.1针对问题1和2

问题一中需要求解人在奔跑的时候会淋多少雨。当前的环境是无风环境，即假定雨只有垂直方向${V_r}$。行人的速度固定为v，已经假定了行人的前进方向的等效面积为${S_h}$和顶部面积为${S_v}$。则将淋雨问题分拆成两个问题：顶部面积的受雨量和侧部面积的受雨量分别进行考虑。

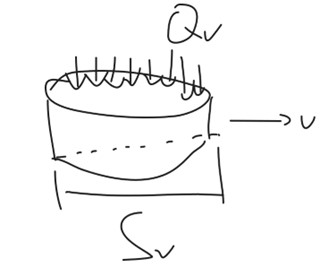
顶部面积可以假想此时有一个横截面积为${S_v}$的水盆，水盆一直在以匀速直线运动向前移动，在移动路径上不停地往里面灌入雨水。基于以上假设，定义雨水在空间中的饱和度为单位体积的空间中雨水的体积${V_w}$（单位时间内打湿的面积比很令人费解，是指一个截面上水的面积占该截面的总面积吗？），则在竖直方向上产生的单位面积流量为$Q_v=V_w*v_r$，则横截面积为Sh的水盆在单位时间内接收到的水量大小为${Q_v}{S_v}$。模型示意图如下图所示：

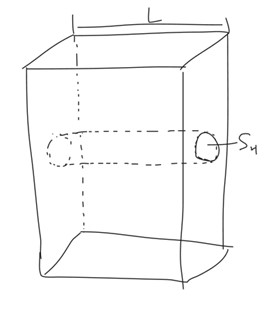
侧部面积的受雨量可以假定为整个的雨幕空间形成了一堵墙，人从起点到终点实际上是在这堵墙中打通一条隧道，打通这条隧道所需要挖土的体积，即是受雨量。设雨在竖直方向上的密度$ {V_w} $，打穿的隧道体积为$ L S_h $ ，则在这条隧道空间中的雨滴总体积为$ LS_h V_w$ 。计算模型如下图所示：

综合以上可以得到人在奔跑过程中，在水平和竖直方向上淋到的雨量公式模型如下所示：

$$ Q(V) = \frac{L}{V}{V_w}{V_r}{S_v} + L{S_h}{V_W} $$

根据以上计算模型，要使得人在到达目的的过程中使得淋雨量最小，则需要使得人奔跑的速度尽可能大。

3.2针对问题3

如果要考虑雨的水平速度的话则需要区分雨在人的奔跑前进方向上的投影速度${V_n}$和与运动速度发现方向投影的速度${V_a}$。基于问题的假设中，人奔跑的运动速度为匀速直线运动v，则在人奔跑的过程中，${V_a}$和${V_n}$始终保持不变为常数。则考虑到人的侧边也有淋雨面积，设人的侧面淋雨面积为${S_s}$，则侧面的情况与顶面的相同，单位时间接收到的水量大小为${V_W}{V_a}{S_s}$。

考虑人的前进方向，在整个运动过程中风的运动方向以人的前进方向为正方向，即若人是顺风奔跑则${V_n}$大于0，逆风奔跑${V_n}$小于0。逆风时可以看做除了挖掘隧道以外，雨还在主动向你靠拢，就像侧面和顶面的计算模型类似。当风速不为定值时，此时人的淋雨模型修改为：

$$ Q(V) = \frac{{{V_W}L}}{V}[{V_r}{S_v} + {V_s}{S_s} + |v - {v_n}|{S_h}] $$

要计算最优速度则需要找到Q(v)的极值，对Q(v)求导，计算得到：

$$ \frac{{dQ}}{{dV}} = {V_w}[ - \frac{L}{{{v^2}}}({v_r}{S_v} + {v_a}{S_s} - {v_n}{S_h})],v - {v_n} > 0 $$

$$ \frac{{dQ}}{{dV}} = {V_w}[ - \frac{L}{{{v^2}}}({v_r}{S_v} + {v_a}{S_s} - {v_n}{S_h})],v - {v_n} < 0 $$

考察得到淋雨量极值与人奔跑的速度v成二次反比例关系，且对于v来说不存在极值点。$\frac{dQ}{dv}$增减与雨滴在人的前进路径上的切向（沿速度方向）速度有关。

根据以上计算结果，定义一个临界风速$v_{cr}$，该临界速度决定了淋雨量是增函数还是减函数。

$${v_r}{S_v} + {v_a}{S_s} \pm {v_{cr}}{S_h} = 0$$

$$ => {v_{cr}} = \pm \frac{{{v_r}{S_v} + {v_a}{S_s}}}{{{S_h}}} $$

考察奔跑速度与实际风速的关系，当奔跑速度大于实际风速时，此时风为顺风，但是人跑的比风快，仍然是前面淋雨；或此时风为逆风，人在奔跑时也是前面淋雨。此时套用公式①，得到：

$$ => {v_{cr}} = \frac{{{v_r}{S_v} + {v_a}{S_s}}}{{{S_h}}} $$

进一步分析：

1. 当$v_n$大于$v_{cr}$时，风速由顺风风速不断增大，则Q变成了增函数，随着v的增大而增大；
2. 当$v_n$小于$v_{cr}$时，此时顺风风速不断减小，渐渐转变为逆风，此时Q为减函数，随着v的增大而减小；
3. 当$v_n$等于$v_{cr}$时，淋雨量导数恒为0，即当奔跑速度满足大于$v_n$的条件时，淋雨量与奔跑速度无关。

当奔跑速度小于实际风速时，若风为顺风，人跑的比风慢，则是后背淋雨；若风为逆风，人在奔跑时则是前面淋雨。此时套用公式②，得到:

$$ => {v_{cr}} = - \frac{{{v_r}{S_v} + {v_a}{S_s}}}{{{S_h}}} $$

进一步分析：

1. 当$v_n$大于$v_{cr}$时，风速由顺风不断增大，Q变为了减函数，随着v的增大而减小；
2. 当$v_n$小于$v_{cr}$时，风速由顺风不断减小，直到逆风，Q变为了增函数，随着v的而增大；
3. 当$v_n$等于$v_{cr}$时，淋雨量导数恒为0，即当奔跑速度满足大于0小于$v_n$的条件时，淋雨量与奔跑速度无关。

当雨滴在人奔跑的切线方向上的投影等于该临界速度时，将不再受到前进方向上的水平向淋雨；当雨滴在人奔跑的切线方向上的投影小于该临界速度时，人是前侧淋雨；当雨滴在人奔跑的切线方向上的投影大于该临界速度时，人是背后淋雨。

根据以上结论可以得到：

1. 存在一个临界风速$v_{cr}$使得人奔跑时候的淋雨量与人的运动速度无关；
2. 当人奔跑的速度v较小时，如实际风速小于临界风速，淋雨量随着奔跑的速度的增大而增大；反之则减小；
3. 当人奔跑的速度v较大时，实际风速小于临界封堵，淋雨量随着奔跑的速度增大而减小，反之则增大。 因此人在决定奔跑前应该首先测量一下风速，如果风速较大且顺风的话，应该尽可能地跑快；如果风速较小且顺风的话应该奔跑速度应该保持和风速差不多。如果风速较大为逆风的话，人应该尽可能地跑快。

3.3针对问题4

以上测定降雨量考察了假定了雨滴在空间中是均匀分布的，而雨滴由于空气阻力和重力的共同作用下，在近地附近的垂直方向速度是基本恒定的，因此可通过测定单位面积单位时间情况下，收集到的水的体积，假定雨滴的体积密度为$V_w$，则雨滴下落的速度可以通过上面的流量体积公式进行反算。

由于雨滴的体积密度难以测量，因此当前学术界和工业界描述降雨量一般是单位面积单位时间收集到的水面高度来划分不同级别的雨量。

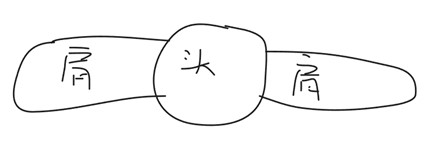
对于雨水打湿面积来说，人体淋雨部分的外表面均被淋湿，当人向前奔跑，且是逆风时，人的后背不会被雨淋湿（头顶上滴下来不算，假定全被盆子装了）。安装人体外表面分别在水平方向上投影，可以得到一个葫芦形轮廓，如下图所示：

同理，人奔跑的法向面淋雨投影面：

奔跑方向的切向方向投影面：

3.4对于问题5

问题5需要给出不同天气下的奔跑建议，基于以上的分析结果，当天气无风时为了减少淋雨，则奔跑的速度自然是越大越好；若天气有风，则需要结合沿着前进方向上的风速综合考虑。

由于Q的表达式只与L成正比例的关系，因此不论路程的长度均可以执行相同的策略：顺风前进的话应该尽可能地保持前进速度与风速相同，逆风前进的话，尽可能地赶紧跑就对了！要注意雷雨天气不要外出哦~

4模型的进一步改进

如果行人奔跑的路径不是直线的情况，则有一点的变化。假定从起点出发，在终点处的路程为，人行走的速度为v(t)此时v是一个随时间变化的矢量，等于$v(t)=v_x i+ v_y j$，速度与x轴的夹角为$\tan \theta = \frac{{{v_y}}}{{{v_x}}}$。假定花费的总时间为$t_0$，则满足如下关系式$\int_0^{{t_0}} {\sqrt {{v_x}^2 + {v_y}^2} dt} = L$。

由于奔跑的速度方向不再恒定，则风速在奔跑速度的切线方向与法向方向上的速度也不再恒定，假定风的速度为$v_w$，可以表达成在x轴和y轴的投影和的形式：$v_a=v_{wx}i+v_{wy}j$，与x轴方向的夹角为： $\tan \varphi = \frac{{{v_{wy}}}}{{{v_{wx}}}}$ 。

风速与奔跑速度的夹角为：$\theta (t) - \varphi (t)$夹角模型示意图如下图所示：

风速在奔跑切线方向上的投影为：

$$ {v_a} = {v_w}\cos (\theta (t) - \varphi (t)) $$

风速在奔跑切向方向上的投影为：

$$ {v_n} = {v_w}\sin (\theta (t) - \varphi (t)) $$

基于3.2节中提出的流量公式，进一步改进：

$$ Q(v) = {V_w}\int_0^{{t_0}} {{v_r}{S_v} + {v_a}{S_s} + |v - {v_n}|{S_h}dt} $$