1 Rayleigh-Ritz法的基本概念和求解步骤

弹性力学的中的Rayleigh-Ritz法本质上是一种考虑物理规律的数值计算方法，通过数值逼近的方法计算力学问题的近似解。这样可以在求解复杂的力学问题中绕开直接求解复杂的偏微分方程，基于力学的基本原理对求解过程进行简化，绕开无法直接求解的数学问题。在弹性力学问题中，常用的数值计算方法有有限单元法（Finite Element Method, FEM）、有限差分法（Finite Difference Method, FDM）和离散单元法（Discrete Element Method, DEM）。其中采用FEM和FDM求解工程力学问题时，均使用的是考虑物规律的数值计算方法，主要包括三种Rayleigh-Ritz法、Strong Form Galerkin (SFG)法和Weak Form Galerkin (WFG)法。本文将主要介绍Rayleigh-Ritz法的基本原理和求解过程。

1.1 弹性力学中的最小势能原理

定义：在弹性问题中，所研究的弹性系统在处于平衡状态下的总势能，恒小于这个弹性系统在其他运动状态下的总势能。

在定义中有一个重要概念：总势能。弹性系统中的总势能等于弹性系统中的所有变形势能减去外力对弹性系统的做功。在不考虑有势体积力作用的情况下，总势能的计算表达式为：

$$ \Pi \left(u_{i}\right)=U-W=\frac{1}{2} \int_{\Omega } \sigma_{ij} \epsilon_{ij} d\Omega -\int_{\Omega } \bar{p}_{i} u_{i}d\varGamma $$

其中：$\Pi$为弹性系统的总势能函数，$u_i$为弹性系统中每个单位微元的位移，$\Omega$为弹性系统包含的区域，$\sigma_{ij}$为单元在指定方向上的应力，$\epsilon_{ij}$为单元在指定方向上的应变，$\bar {p_i}$为单元$i$受到的外力，$u_i$为单元$i$的位移。

基于最小势能原理可以得到弹性体系存在一个位移形式，在这个位移形式下弹性体系的总势能取到最小值，由于这个最小值在连续函数中也是极小值，因此认为当前的位移形式为总势能函数的极值点。即有：

$$ \int_{\Omega } \left| \frac{\partial \Pi }{\partial u_{i}} \right| d\Omega =0 $$

1.2 Rayleigh-Ritz法的求解步骤

基于最小势能原理，Rayleigh-Ritz法的核心计算思路为：假定弹性体系的位移形函数，计算在当前假定的位移形函数下的总势能表达式，计算满足最小势能原理时的位移形函数。具体的计算步骤如下：

1. 根据边界条件（Boundary Condition）建立位移形函数的表达式；
   1. 弹性力学中的常用边界条件有两种：Essential Boundary Condition (EBC, 位移边界条件)，Natural Boundary Condition （NBC，受力边界条件），在Rayleigh-Ritz法中需要保证定义的位移形函数满足EBC条件；
   2. 位移形函数一般选用完备函数的级数，如多项式级数、三角函数级数、小波技术、傅立叶级数等，对于二维变形三维变形等情况同样适用；
   3. 若使用位移形函数描述二维问题时，如悬臂梁、简支梁等，则在定义位移形函数时需要让位移形函数满足体系的边界条件，如悬臂梁在在$x=0$处的位移为0，则悬臂梁的变形曲线可以描述为：$w(x)=\sum^{n}_{i=1} a_{i}x^{i}$，保证悬臂梁的固定处满足$w(0)=0$
   4. 若使用位移形函数描述二维甚至多维问题时，如板的变形，体的变形，同样需要满足边界条件，且在Rayleigh-Ritz法的计算过程中必须保证定义的边界条件为EBC；

2. 计算弹性体系在当前的位移形函数下的应变能；

   1. 对于二维问题，一般应用Rayleigh-Ritz法计算弯曲变形梁的应变能，需要根据梁的厚高比选取合适的梁模型，常用的梁模型包括Euler-Bernoulli梁和Timoshenko梁模型，主要区别在于Timoshenko梁模型考虑梁的剪切应变能；
   2. Euler-Bernoulli梁模型的应变能表达式为$U_E=\frac{EI}{2}\int_0^L (\frac{d^2u}{dx^2})dx$;
   3. Timoshenko梁模型的应变能表达式为$U_T=\frac{EI}{2}\int_0^L{(\frac{d^2u}{dx^2})dx} + \frac{\alpha(EI)^2}{2GA}$，其中$\alpha_s$为不均匀剪切系数，$\alpha_s = \frac{A}{I^2}\int_A \frac{S^2}{b^2}dA$，其与截面形式有关，一般矩形截面取为$\alpha_s = \frac{6}{5}$
   4. 对于三维问题，一般应用Rayleigh-Ritz法计算板的应变能，需要根据板厚度和两个方向的尺度比选取合适的板模型，比较常用的是高阶剪切板理论，这里介绍一下我副导师文章中提出的（General Third-Shear Deformation Plate Theory）
   5. 剪切板理论的变形能计算方法：
   $$U=\frac{EI}{2} \int_{\Omega }{ \left( \frac{\partial^{2} w}{\partial x^{2}} +\frac{\partial^{2} w}{\partial y^{2}} \right) -2\left( 1-\nu \right) \left( \frac{\partial^{2} w}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} -\left( \frac{\partial^{2} w}{\partial x\partial y} \right)^{2} \right) dxdy} + U_s$$
   1. 其中$U_s$是考虑剪切效应的剪切应变能。
   2. 当所选用的剪切板模型GTSDPT时，剪切应变能的计算表达式为：

$$ U_{s}=G\int_{\Omega }{ \left( \frac{\partial u}{\partial y} +\frac{\partial v}{\partial x} +z\frac{\partial \theta }{\partial y} +z\frac{\partial \varphi }{\partial x} \right) +\left( \theta +\frac{\partial w}{\partial x} \right)^{2} +\left( \varphi +\frac{\partial w}{\partial y} \right)^{2} d\Omega } $$

3. 计算弹性体系受到的外力做功，若弹性体的变形与外力的变形一致，则外力做正功，否则做负功。弹性体系的变形能按照总势能表达式的中的方程进行计算； 4. 计算获得总势能表达式后，假定位移形函数中的待定系数的集合为${a_i}$，对弹性体系总势能计算关于位移形函数的关于待定系数的变分：

$$ \frac{\partial \Pi }{\partial a_{i}} =0 $$

5. 求解代数方程组，获得待定系数，将待定系数代入至位移形函数中，获得弹性体系的位移函数。 ## 1.3 算例 如图所示是一个悬臂梁模型，梁的长度为$L=3m$，一端固定在墙上，一端自由。梁上分布了$2kN/m$的均布荷载，计算梁的挠度函数。  ### 1.3.1 材料力学解法 在材料力学中，基于弹性、各向同性、连续性、小变形等假定，在欧拉梁模型下，梁的挠度与受力关系满足以下基本假定：

$$ \frac{d^2w(x)}{x} = - \frac{M(x)}{EI} $$

其中：$w(x)$为材料力学中梁的挠度函数，$M(x)$为材料力学中梁的弯矩函数。

首先计算梁的剪力函数：

$$ F_s(x) = 30 - 10x $$

对剪力进行积分，代入$x=3$时， 弯矩为0的边界条件，计算过程如下：

$$ M(x) = \int_0^x 30 - 10x dx\\ = 30x - 5x^2 + C \\ $$

代入$M(3) = 0$：

$$ M(3) = 90 - 45 + C = 0 \\ => C = -45 \\ M(x) = 30x - 5x^2 - 45 $$

由挠度和弯矩的关系，并代入固定端的挠度和转角为0的边界条件，有：

$$ \theta(x) = \frac{dw}{dx} = -\frac{\int_0^x 30x - 5x^2 - 45dx}{EI} \\ =\frac{15x^2 - \frac{5}{3} x^3 - 45x + C}{EI} \\ \theta(0) = -\frac{C}{EI} = 0 \\ => \theta(x) = -\frac{15x^2 - \frac{5}{3} x^3 - 45x}{EI} $$

进一步进行积分，并代入边界条件$w(0)=0$得到：

$$ w(x)=\int_0^x \theta(x)dx=-\frac{5x^3-\frac{5}{12}x^4-\frac{45}{2}x^2}{EI} \\ =-\frac{5x^3-\frac{5}{12}x^4-\frac{45}{2}x^2}{2E4} $$

最大变形位置发生在$x=3$处，最大变形大小为：

$$ w(3) = 0.0050625m = 5.0625 mm $$

1.3.2 Rayleigh-Ritz法解法

使用高阶多项式拟合梁的变形曲线，多项式的级数项数越高，计算结果越精确，这里同材料力学方法中的计算结果，选取4阶多项式，满足两个位移边界条件，固定端的挠度为0，转角为0：

$$ w(x) = a_0x^2 + a_1x^3 + a_2x^4 $$

多项式中包含5个待定系数$a_i$。应用欧拉梁的模型计算梁在当前变形下的变形能：

$$ U = 120000.0 a_{0}^{2} + 1080000.0 a_{0} a_{1} + 4320000.0 a_{0} a_{2} + 3240000.0 a_{1}^{2} + 29160000.0 a_{1} a_{2} + 69984000.0 a_{2}^{2} $$

计算外力做功：

$$ W = \int_0^3 10w(x) dx \\ = 90 a_{0} + \frac{405 a_{1}}{2} + 486 a_{2} $$

构造总势能函数：

$$ \Pi = U - W \\ = 120000.0 a_{0}^{2} + 1080000.0 a_{0} a_{1} + 4320000.0 a_{0} a_{2} - 90 a_{0} + 3240000.0 a_{1}^{2} + 29160000.0 a_{1} a_{2} - \frac{405 a_{1}}{2} + 69984000.0 a_{2}^{2} - 486 a_{2} $$

对所有的待定系数计算总势能变分：

$$ \frac{\partial \Pi}{\partial a_i} = 0 $$

得到以下的方程组：

$$ 240000.0 a_{0} + 1080000.0 a_{1} + 4320000.0 a_{2} - 90=0 $$ $$ 1080000.0 a_{0} + 6480000.0 a_{1} + 29160000.0 a_{2} - \frac{405}{2}=0 $$ $$ 4320000.0 a_{0} + 29160000.0 a_{1} + 139968000.0 a_{2} - 486=0 $$ `

` 求解方程组，得到挠度函数的表达式：

$$ w(x) = 2.08333333333333 \cdot 10^{-5} x^{4} - 0.00025 x^{3} + 0.001125 x^{2} $$

挠度函数的表达式与材料力学计算得到的表达式完全相同，相互验证了两种方法均计算正确。

1.3.3 灵敏度分析

令选取的多项式次数为3次和五次，分别计算变形曲线表达式：

$$ w_3(x) = - 0.000125 x^{3} + 0.0009375 x^{2} \\ w_4(x) = 2.08333333333333 \cdot 10^{-5} x^{4} - 0.00025 x^{3} + 0.001125 x^{2}\\ w_5(x) = 2.08333333333333 \cdot 10^{-5} x^{4} - 0.00025 x^{3} + 0.001125 x^{2} $$

绘制三个多项式的变形曲线，如下图所示。

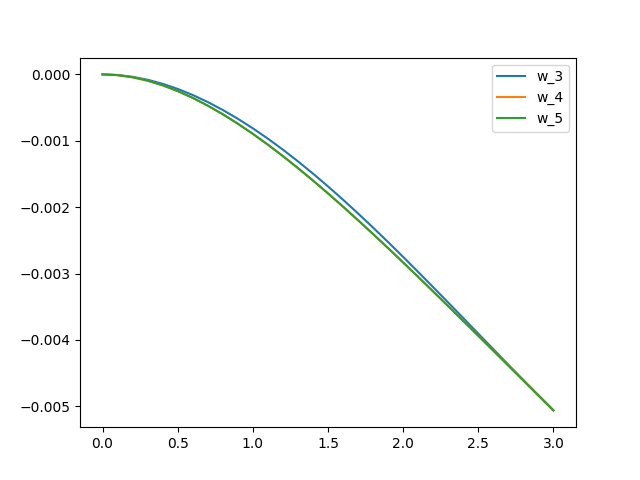
可以看到所选取的位移函数在次数较小时仍有较高的计算精度，但是对于简单问题来说存在一个上限精度。当选取的多项式超过该上限精度后，计算的准确度无法再进一步提升，因此在实际计算中应合理选择构造位移函数的的精度以达到算法的性能与精度的平衡。