0引言

随着我国的城市化进程的快速推进，人口越来越向城市中心聚集，导致城市的土地资源日趋紧张。因此，为提高土地的利用率、缓解城市资源紧张，城市的地下空间开发成为了当前城市土地利用的新趋势。尤其是城市轨道交通工程和大型建筑配套的大型地下室等项目都离不开深基坑工程的发展。内撑式支护结构指使用内部横向支撑或角支撑与挡土结构协同作用，以起到限制位移、提高生产安全系数的作用。
如今，城市地下空间结构的复杂度越来越高，以及城市基坑建设的要求和场地的使用限制越来越严格，内撑式基坑支护结构面临非对称荷载作用的情形也越来越多。内撑式基坑支护面临的非对称荷载的形式比较主要的有基坑两侧堆载差异情形、基坑两侧土质差异情形和开挖深度差异情形。现行的《建筑地基基础设计规范》中没有对非对称荷载情形做差异性的设计规定^[1]。

基坑工程事故率比较高和由于支护设计不合理造成的工程费用偏大是目前基坑工程发展中存在的主要问题。一般的设计时，针对非对称荷载情况下的基坑支护安全系数，基坑两侧的支护结构均采取荷载最不利一侧的情况进行设计。而在实际非对称荷载条件下，荷载较小的一侧的土压力更小，支护结构的设计强度仍有盈余^[2]，因此造成工程经济上的浪费。若不采用最不利条件下的支护结构强度进行设计，则目前还没有规范的方法用以较为准确地计算荷载较小一侧所需的支护结构强度。同时，在基坑两侧加装水平横向内撑后，荷载较大一侧发生变形。该作用通过水平横向支撑传递到荷载较小一侧会使得荷载较小一侧的变形形式产生一定的有利作用^[3]。同时，随着建设要求的不断提高，设计方案也逐渐从强度控制转变为变形控制，在设计时，需要结合支护结构的变形刚度和强度进行综合考虑。因此针对非对称荷载条件下的土压力分布和支护结构的内力变形性状展开研究十分必要。

本文从一般基坑支护设计方法开始，到非对称荷载条件下的基坑支护结构的变形特性，从中提取其中的共性和特性进行讨论。

1从一般基坑加载状态到非对称开挖加载状态

随着地下空间的大规模开发和利用，工程质量等级的不断提高。现行的《建筑基坑支护技术规程 JGJ120-2012》^[4]中将支护结构的极限状态分为承载力极限状态和正常使用极限状态。而《规范》中对支挡式结构、土钉墙和重力式水泥土墙等的设计相关规范均从对结构承载力计算和稳定性验算出发，而很少考虑到支护结构在不同的环境和工况下的变形效应，如此难以满足当前高等级基坑的变形控制设计需求。基坑隆起变形问题研究中存在的理论分析不够完善, 且远落后于工程实践等不足，进而不少学者开展了对基坑支护变形特性的相关研究和展望^[5][6][7][8]。

2一般基坑加载状态时内撑式基坑支护变形研究

2.1内撑式基坑土压力计算理论

基坑支护结构承受的主要荷载来自于基坑周边土体，在《建筑基坑支护技术规程 JGJ120-2012》[4]中为计算基坑支护结构的水平土压力。一般来说，深基坑项目坑底在地下水位以下，地下水位以下的土体的应力包括有效应力和孔隙水压力，土压力的计算方法十分复杂。同时对于当前的粘性土压力的计算问题，在研究方法上存在水土分离算法和水土结合考虑算法的分歧^[9][10]。

《建筑基坑支护技术规程 JGJ120-2012》给出了水土合算和水土分算的土压力计算公式：

$$ {p_{ak}} = {\sigma _{ak}}{K_{a,i}} - 2{c_i}\sqrt {{K_{a,i}}} $$ $$ {K_{a,i}} = {\tan ^2}(45 - \frac{{{\varphi _i}}}{2}) $$ $$ {p_{pk}} = {\sigma _{pk}}{K_{p,i}} - 2{c_i}\sqrt {{K_{p,i}}} $$ $$ {K_{p,i}} = {\tan ^2}(45 + \frac{{{\varphi _i}}}{2}) $$

式中：${p_{ak}}$为支护结构外侧，第$i$层土中计算点的主动土压力强度标准值($k_{Pa}$)；当$p_{ak} <0$时，应取$p_{ak}＝0$；$σ_{ak},σ_{pk}$分别为支护结构外侧、内侧计算点的土中竖向应力标准值($kPa$)；${K_{a,i}},{K_{p,i}}$分别为第i层土的主动土压力系数、被动土压力系数；${c_i}$,${\varphi _i}$第i层土的粘聚力($kPa$)、内摩擦角(°)；$p_{pk}$──支护结构内侧，第$i$层土中计算点的被动土压力强度标准值($kPa$)。

对于水土分算土层土压力计算公式如下：

$$ {p_{ak}} = ({\sigma _{ak}} - {u_a}){K_{a,i}} - 2{c_i}\sqrt {{K_{a,i}}} + {u_a} $$ $$ {p_{pk}} = ({\sigma _{pk}} - {u_p}){K_{p,i}} + 2{c_i}\sqrt {{K_{p,i}}} + {u_p} $$

其中：$u_a$,$u_p$分别为支护结构外侧、内侧计算点的水压力($kPa$)。综合以上水土分算和合算使用条件，应用以上计算表达式导出基坑围护结构土压力计算模型如下图所示：

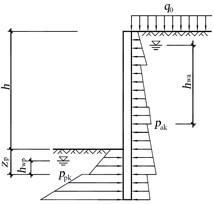
“规范”中规定的土压力计算方法为计算静土压力的方法，当支护结构受到土压力发生变形之后，净土压力即转变为主动土压力和被动土压力，土压力的大小和计算方法发生变化。而当前土力学理论中计算主动土压力和被动土压力的方法主要为朗肯土压力理论和库伦土压力理论，已有的理论计算方法均是假定土体位移已经达到极限状态。在实际工程中，主动土压力的位移极限状态较为容易达到，被动土压力的位移极限状态由于需要较大的土体位移，往往超过工程允许范围。因此有不少研究者针对土体位移未达到极限状态时的土压力理论进行了相关研究^[11][12][13]，当前常用的土体位移修正示意图如下图所示：

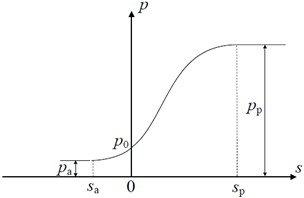
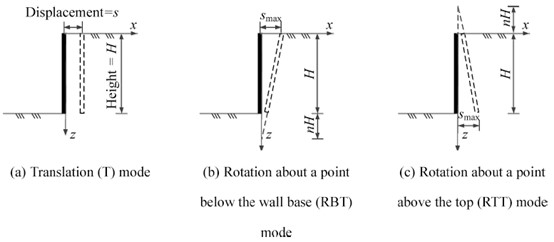
基坑支护结构在土压力，支撑力等综合作用下会发生一定的位移。为了研究支护结构的位移规律并应用以上的土压力系数与支护结构位移的修正关系，当前的研究针对支护结构的变位模式将支护结构的变形分为平动模式（T模式）、绕顶部转动模式（RT模式）、绕底部转动模式（RB模式）。

张恒志等^[14]基于静力平衡方法结合离散元模拟等方法分析了RB模式下的主动土压力分布问题，假定了墙后土体的滑裂线倾角与库伦理论一致，推导了RB模式下有限土体主动土压力的理论计算公式。Fan等^[15]通过假定被动土压力系数与位移呈线性关系，在库伦土压力理论的基础上对被动极限状态下的土压力系数进行了修正，使土压力模型能适应不同的墙体运动，推导了墙体分别在T模式、RT模式、RTT模式、RB模式、RBT模式下的被动土压力系数的计算公式，结合了模型实验得到的实验数据，验证了推导的理论公式的可行性。分别对于以上几种模式总结现有研究提出的主动土压力计算公式和被动土压力计算公式。

RB模式下的主动土压力计算公式：

$$ {p_h} = \left\{ {\begin{array}{*{20}{c}} {{K_1}\gamma z(0 \le z \le {h_1})}\\ {{K_2}\gamma (z - {h_1}) + {K_1}\gamma {h_1}({h_1} < z \le H)} \end{array}} \right. $$

其中：${K_1}$为滑裂面分割线I区三角形计算区域同时也是库伦理论中的主动土压力系数，${K_2}$为滑裂面分割线Ⅱ区计算区域的主动土压力系数，${h_1}$为滑裂面分割线在支护结构上的高度。

$$ {K_1} = \frac{{\sin (\alpha - \varphi )\cos \delta \cot \alpha }}{{\cos (\alpha - \varphi - \varphi )}} $$ $$ {K_2} = \frac{{\cos (\alpha - \varphi + \delta )}}{{\cos (\alpha - \varphi - \delta )}}{K_1} $$ $$ {h_1} = B\tan \alpha $$

其中：$\alpha $为库伦主动土压力滑裂面倾角，计算公式为：

$$ {\alpha _{cr}} = \arctan \left[ {\sqrt {\frac{{\tan \varphi }}{{\tan (\varphi + \delta )}} + {{\tan }^2}(\varphi ) + \tan (\varphi )} } \right] $$

主动土压力的计算模型如下图所示：

RB模式下的被动土压力计算公式为^[16]：

$$ {p_{RB}} = ({K_p} - {K_0})\gamma \left( {\frac{3}{{2 - 3m}}\frac{{{z^2}}}{H} - \frac{{3m}}{{2 - 3m}}z} \right) + {K_0}\gamma z $$

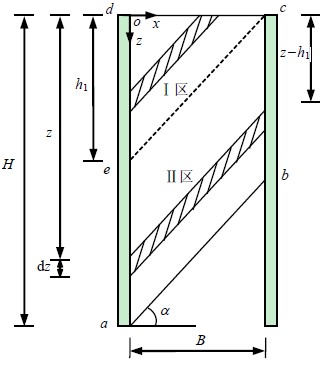
其中：${K_p}$为被动极限状态下的库伦土压力系数；$K_0$为静土压力系数，$m = x/H$为旋转中心的参数。

$$ {K_p} = \frac{{{{\cos }^2}\varphi }}{{{{(\sqrt {\cos \delta } - \sqrt {\sin (\delta + \varphi )\sin \varphi } )}^2}}} $$

T模式下的未达到极限状态和极限状态的被动土压力的计算公式：

$$ {p_T} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\left( {{K_p} - K_0} \right)\frac{s}{{{s_p}}} + {K_0}} \right]\gamma z}&{s \le {s_p}}\\ {{K_p}\gamma z}&{s > {s_p}} \end{array}} \right. $$

其中：${K_p}$为被动极限状态下的库伦土压力系数；$K_0$为静土压力系数；$s$为土体位移大小；$s_p$为主动土压力极限位移大小。

RBT模式下的被动土压力计算公式如下式所示：

$$ {p_{RBT}} = \left\{ {\begin{array}{*{20}{c}} {{K_p}\gamma z}&{0 \le z \le (1 - \frac{{{s_p}}}{{{s_{\max }}}})H}\\ {\left( {{K_0} - ({K_0} - K{'_p})\frac{{{s_{\max }}}}{{{s_p}}}\frac{{H - z}}{H}} \right)\gamma z}&{(1 - \frac{{{s_p}}}{{{s_{\max }}}})H \le z \le H} \end{array}} \right. $$

其中：$K{'_p}$为RBT模式下的修正土压力系数；${s_{\max }}$为支护结构的最大位移大小。

$$ K{'_p} = - \frac{2}{{1 + 3n}}{K_0} + \frac{{3 + 3n}}{{1 + 3n}}{K_p} $$

其中：$n$为插入深度比。

RTT模式下的被动土压力计算公式如下式所示^[17]：

$$ {p_{RTT}} = \left\{ {\begin{array}{*{20}{c}} {(K{'_p} - {K_0})\frac{{z + nH}}{{(n + 1)H}}\frac{{{s_{\max }}}}{{{s_p}}}\gamma z + {K_0}\gamma z}&{{s_{\max }} \le {s_p}}\\ {\begin{array}{*{20}{c}} {\left( {{K_0} - ({K_0} - K{'_p})\frac{{{s_{\max }}}}{{{s_p}}}\frac{{z + nH}}{{(n + 1)H}}} \right)\gamma z}&{0 \le z \le (n + 1)\frac{{{s_p}}}{{{s_{\max }}}}H - nH}\\ {{K_p}\gamma z}&{(n + 1)\frac{{{s_p}}}{{{s_{\max }}}}H - nH \le z \le H} \end{array}}&{{s_{\max }} > {s_p}} \end{array}} \right. $$

以上主动土压力计算模型如下图所示：

2.2内撑式基坑支护结构变形理论

按照材料力学理论和结构力学理论，支护结构的变形主要受两项主要因素的影响——支护结构本身的刚度和支护结构受到的外力。基于2.1节，综合近年的研究总结了基坑支护结构的土压力一般计算方法。对于内撑式基坑支护结构，当前也有部分学者针对其分部刚度和整体刚度进行了相关研究。

当前业内主流的支护结构整体刚度的计算体系主要为Clough 支护刚度^[18][19]及其各种相关改进方法。Clough刚度体系是Clough等在1989年开创性提出的 $ EI/({\gamma _w}{h^4}) $ 公式，用于反映基坑围护的无量纲综合刚度。其中$EI$为围护墙（桩）刚度，$h$为支撑竖向平均间距，${\gamma _w}$为水的重度。Clough的无量纲综合刚度的提出，将基坑围护刚度的研究从单一因素提升至综合因素的高度，即在一个围护结构刚度公式中同时包含了围护墙（桩）刚度与支撑竖向间距两个变量。其表示的综合刚度最大侧向位移${\delta _{\max }}/H$关系曲线如下图所示：

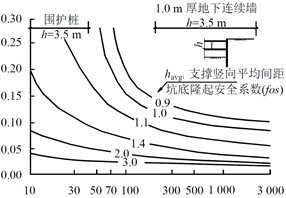
另外，也有很多的研究者针对基坑支护结构的变形状态本身进行了研究。如周松等^[20]以成都春熙路地铁车站深基坑为背景对基坑内撑式支护结构的内力和变形展开了研究，结合Midas/GTS建立基坑三维模型进行了动态数值模拟，并结合现场实测数据同设计值进行了对比分析，得到：

1. 在安装第一道钢支撑前，桩身变形桩顶较小，桩底变形较大，排桩呈直线向基坑内偏移。施工第二道钢支撑后，桩身变形整体呈“凸”型，且桩顶位移较小，桩底位移向基坑外偏移较大，中部向坑内变形。

2. 钢支撑的施加能够控制排桩向基坑内的变形。钢支撑轴力模拟值与监测值接近，而设计值偏大；排桩弯矩、剪力监测值与设计结果较为吻合。

3. 增加钢支撑刚度、预加轴力和排桩自身刚度，可以有效的抑制排桩水平位移，同时也会使得排桩弯矩增加，内支撑轴力逐渐减小。

4. 随着泥岩粘聚力、内摩擦角、弹性模量减小或泊松比的增加，排桩中下部位移都会一定程度的增加。其中，泥岩泊松比对排桩的水平位移的影响最大，其次为弹性模量、内聚力、内摩擦角。

结论得出：施加第二道支会改变支护结构的变形状态，支撑刚度增加能够有效抑制支护结构变形，但是会增加支护结构的内力。

另外有大量学者针对开挖基坑的其他力学形状进行了研究，如E. Conte等^[11]根据考虑开挖后的无粘土的力学特征，结合数值分析和模型试验得推导了悬臂式挡土墙的受力变形特性理论公式。Xuhe等^[21]使用MIDAS/GTS NX中对基坑开挖过程进行了三维数值模拟，同时结合监测数据指出：圆形地下连续墙周围地表的沉降主要是由基坑开挖深度决定的，各工况的壁面变形均呈线性关系，具有明显的阶段性特征。尤其是变形曲线有明显的拐点，大部分拐点位于总开挖深度的2/3以上。A. Girgidov^[22]结合基坑开挖，研究了基坑降水的时间特性，并推到了相关公式。L. JC^[23]等结合现场检测数据和有限元分析结果，分析了基坑开挖失效的状态，并总结了之后相关工程的避免方法。C. Kang等^[24]基于弹性力学的方法提出了一种预测基坑开挖引起的地面横向位移的简化方法，指出随着土壤与支撑结构物的距离增加，最大地面横向位移呈非线性减小，主要受基坑支护结构的形式和结构影响。L. Mian等^[25]考虑深基坑的竖向支撑系统的横向承载力，结合数值分析和相关力学原理，提出了一种基于数值分析结果的侧向刚度计算方法，可以应用到设计中充分考虑支护结构的承载力，提高经济效益。

3非对称开挖内撑式基坑支护结构变形的共性与个性

为了确保基坑支护体系的安全性及经济性，其设计理论的研究至关重要。《建筑基坑支护技术规程JGJ120-2012》^[4]中规定：对每一计算剖面，应按其最不利条件进行计算。而实际上在荷载水平较低的一侧，应用与最不利条件进行设计在保证相同的安全系数下，其经济效益更低。同时由于基坑工程的不断发展，基坑支护体系的设计控制原则由承载力控制方法逐渐转为变形控制原则。因此，为了研究非对称开情况下支护结构的变形特性，同时也为了在基坑支护结构设计时提高经济效益，不少研究者针对基坑的非对称开挖形式及基坑支护结构的变形特性、基坑周边土体变形特性等进行了相关研究。以下将从非对称开挖下与对称荷载下的基坑支护变形规律的共性与特性分别做总结。

3.1非对称内撑式支护结构变形的共性

在近年的考虑一般基坑的力学特性研究和在非对称开挖下的基坑力学特性的相关研究中，发现两类研究有一个主要的共同点——基坑支护结构受到的土压力的计算方法相同^{[11][17][26][27]}。事实上，对于非对称开挖来说，开挖过程并未改变基坑外土体的受力特征，同时非对称开挖对与基坑内的土体的主要区别为卸荷比不同，因此在研究基坑内非对称开挖土体的力学特性可以将其考虑为不同的卸荷作用下的土体力学特性。

非对称挖深两侧的支护结构之间会相互影响，可以根据它们之间的相互作用关系建立整体受力变形分析模型^{[3][22][23][28][29][31]}。因此在2.2节中介绍的支护结构整体设计方法仍然适用。

3.2非对称内撑式支护结构变形的个性

当前对于非对称开挖的基坑力学性状的研究较少，且没有形成完整的研究和设计的理论体系，因此主要结合现有的研究成果，针对与一般基坑设计方法的研究结论差异进行分析。

3.2.1非对称支护结构的变形特性

非对称开挖后的基坑，其两侧的支护结构会随着两侧的挖深差异而发生变形差异，且横向支撑的刚度会发生改变^{[2][3][32][33][34]}。相关研究结论可以总结为以下几点：

1. 挖深较深一侧的支护结构平动变形更大，同时随着平动的增加横向支撑的等效轴向刚度逐渐减小；而在挖深较浅的一侧，随着平动变形的增加，支撑的不动点系数逐渐减小。且随着挖深的增加，挖深较深侧的支护结构变形持续增大，挖深较浅侧的支护结构变形增大较缓。

2. 在非对称开挖基坑支护的设计中可以通过调整截面的尺寸和嵌固深度来减小非对称变形对刚度和稳定性变化的影响。

3. 两侧挖深差对开挖较深侧坑外地表沉降影响很大，当两侧挖深差增大时开挖较深侧坑外地表沉降会急剧增大；而开挖较浅侧坑外地表沉降会接近线性增大，且增量较小。

4. 开挖分界面对坑底中间部分隆起的影响较大，而对两边靠近支护结构的隆起的影响很小，且隆起最大值的位置不随开挖分界面的改变而改变。随着两侧荷载差的不断增大，两侧坑外地表沉降的差值也不断增大，与相应对称开挖的差值也越大；随着非对称荷载位置距基坑的距离不断增大，两侧坑外地表沉降的变化较小。

3.2.2非对称支护结构的受力特性

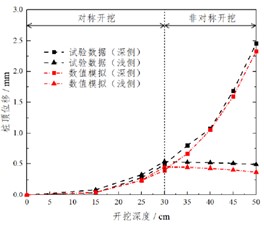
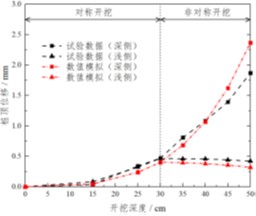
非对称开挖的内撑式基坑支护结构有一个比较重要的特性——变形较大的一侧支护结构对变形较小的一侧通过横向支撑会产生一定的推回作用。关于非对称开挖的桩长对称和桩长非对称的模型试验和数值模拟结果如图6所示：

由图可见，两种工况下，两侧支护结构的桩身变形均近似于刚性变形，呈现桩顶位移最大，沿深度逐渐减小的变形规律。随着开挖深度的增大，深侧支护结构的桩身变形不断增大，且增大速率逐渐增快，而浅侧支护结构在对称开挖时桩身变形不断增大，在非对称开挖时由于受到深侧支护结构通过支撑传递的“推回位移”，桩身变形有所减小。同时，可以观察到，深侧支护结构的桩底存在向坑外方向的位移，说明其转动点位于桩底附近；而浅侧支护结构均为向坑内方向的位移，在桩底附近位置桩身变形接近于零。

4小结

本文总结结构为基于一般基坑的设计方法，引入非对称开挖基坑的特点，并结合今年来相关的非对称开挖基坑工程的相关研究，对当前的非对称开挖支护结构的设计方法进行了一点的总结，主要为以下几点：

1. 基坑开挖的后，作用在支护结构上的土压力往往是非极限状态的，因此在计算时应当考虑做非极限状态进行设计。

2. 内撑式基坑支护变形理论的核心是支护结构的变形刚度。其中当前大部分的基坑支护结构的变形刚度理论均基于Clough综合刚度模型推导得到，且根据不同的工况存在不同的计算变体。

3. 一般基坑支护结构的内力和变形与非对称开挖状态下的内力变形主要有两大共同点：（1）土压力的计算方法相同；（2）支护结构的刚度模型相似。

4. 非对称开挖状态下的基坑支护变形特性的主要特性有：不同挖深侧的支护结构变形特性不同；受力特性主要包括不同变形差异的横向支撑推回作用。

参考文献

1. 中国建筑科学研究院, 建设综合勘察设计研究院, 北京市勘察设计研究院, et al. 建筑地基基础设计规范 [M]. 中华人民共和国国家标准. 2011: 347p:A4. ↩
2. 罗志元. 内撑式非对称开挖条件下的基坑变形研究 [D]; 浙江大学, 2012. ↩
3. 殷铭. 非对称开挖基坑内撑式围护结构受力及变形分析 [D]; 浙江大学, 2016. ↩
4. 中国建筑科学研究院, 中冶建筑研究总院有限公司, 华东建筑设计研究院有限公司, et al. 建筑基坑支护技术规程 [M]. 行业标准-建筑工业. 2012: 220P.;B5. ↩
5. 李平, 杨挺, 王义, et al. 基坑工程隆起变形研究综述 [J]. 河海大学学报: 自然科学版, 2010, 38(2): 196-201. ↩
6. 杨光华. 土钉支护技术的应用与研究进展 [J]. 岩土工程学报, 2010, 32(1): 9-16. ↩
7. XIAO J, DAI F, WEI Y, et al. Analysis of mechanical behavior in a pipe roof during excavation of a shallow bias tunnel in loose deposits [J]. Environmental Earth Sciences, 2016, 75(4): 293. ↩
8. XU C, XU Y, SUN H, et al. Characteristics of braced excavation under asymmetrical loads [J]. Mathematical problems in engineering, 2013, 2013( ↩
9. 李广信. 基坑支护结构上水土压力的分算与合算 [J]. 岩土工程学报, 2000, 22(3): 348-52. ↩
10. 陈愈炯, 温彦锋. 基坑支护结构上的水土压力 [J]. 岩土工程学报, 1999, 21(2): 4-8. ↩
11. CONTE E, TRONCONE A, VENA M. A method for the design of embedded cantilever retaining walls under static and seismic loading [J]. Geotechnique, 2017, 67(12): 1081-9. ↩
12. LIU, H. Required reinforcement stiffness for vertical geosynthetic-reinforced-soil walls at strength limit state [J]. Geotechnique, 2016, ↩
13. MING-XI O U, LIU X R, SHI J X. Earth pressure applied in retaining wall of deep foundation pit considering influence of unloading and deformation [J]. Journal of Central South University(Science and Technology), 2012, 43(2): 669-74. ↩
14. 张恒志, 徐长节, 梁禄钜, et al. RB 模式下刚性挡墙有限土体主动土压力的 离散元模拟与理论研究 [J]. 岩土力学, 42(10): 2895-907. ↩
15. FAN D-L, HUANG L. The Effect and Application of Spatial Effect on the Asymmetrical Deep Excavation [J]. Electronic Journal of Geotechnical Engineering, 2016, 21(1063-78. ↩
16. PENG S Q, XI-BING L I, FAN L, et al. A general method to calculate passive earth pressure on rigid retaining wall for all displacement modes [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(6): 1526-32. ↩
17. FAN X-Z, XU C-J, LIANG L-J, et al. Analytical solution for displacement-dependent passive earth pressure on rigid walls with various wall movements in cohesionless soil [J]. Computers and Geotechnics, 2021, 140(104470. ↩
18. TURNER M J, CLOUGH R W, MARTIN H C, et al. Stiffness and deflection analysis of complex structures [J]. journal of the Aeronautical Sciences, 1956, 23(9): 805-23. ↩
19. CLOUGH G W, SMITH E M, SWEENEY B P. Movement control of excavation support systems by iterative design; proceedings of the Foundation engineering: Current principles and practices, F, 1989 [C]. ASCE. ↩
20. 周松. 深基坑内撑式排桩支护结构变形及内力研究 [J]. 成都理工大学, 2017, 1-z. ↩
21. GAO X, TIAN W-P, ZHANG Z. Analysis of deformation characteristics of foundation-pit excavation and circular wall [J]. Sustainability, 2020, 12(8): 3164. ↩
22. GIRGIDOV A. The time of groundwater free surface lowering before foundation pit construction [J]. Magazine of Civil Engineering, 2012, ↩
23. JC L. Use of 3D finite element method for back study of a failed basement excavation in soft clay [J]. Japanese Geotechnical Society Special Publication, 2016, 2(73): 2504-7. ↩
24. KANG C, XU R, YING H W, et al. Simplified method for calculating ground lateral displacement induced by foundation pit excavation [J]. Engineering Computations, 2020, ahead-of-print(ahead-of-print): ↩
25. MIAN L, YANG X, BO Z. RESEARCH ON LATERAL STIFFNESS OF STRUTTED RETAINING STRUCTURE FOR DEEP EXCAVATION [J]. 工程地质学报, 2020, 28(5): 1116-22. ↩
26. CHUNLIN H, LI C, RENAN L, et al. Monitoring technique and danger situation forecast during the excavation of deep foundation pit [J] [J]. Rock and Soil Mechanics, 1996, 2( ↩
27. CHEN X, XU W, DUAN C. Numerical study on asymmetric excavation-induced supporting structure effect of∞-shape super deep foundation pit; proceedings of the 2011 International Conference on Electric Technology and Civil Engineering (ICETCE), F, 2011 [C]. IEEE. ↩
28. 王宁. 深基坑开挖变形神经网络监测模型研究 [D]; 上海交通大学, 2009. ↩
29. 徐长节, 殷铭, 胡文韬. 非对称开挖基坑支撑式围护结构解析解 [J]. 岩土力学, 2017, 38(08): 2306-12. ↩
30. 尹骥, 管飞, 李象范. 直径210m超大圆环支撑基坑设计分析 [J]. 岩土工程学报, 2006, S1): 1596-9. ↩
31. 张戈, 毛海和. 软土地区深基坑围护结构综合刚度研究 [J]. 岩土力学, 2016, 37(5): 8. ↩
32. 王飞阳. 内撑式非对称基坑支护体系性状分析 [D]; 华南理工大学, 2016. ↩
33. FAN X-Z, PHOON K-K, XU C-J, et al. Closed-form solution for excavation-induced ground settlement profile in clay [J]. Computers and Geotechnics, 2021, 137(104266. ↩
34. 徐长节, 成守泽, 蔡袁强, et al. 非对称开挖条件下基坑变形性状分析 [J]. 岩土力学, 2014, 35(07): 1929-34. ↩